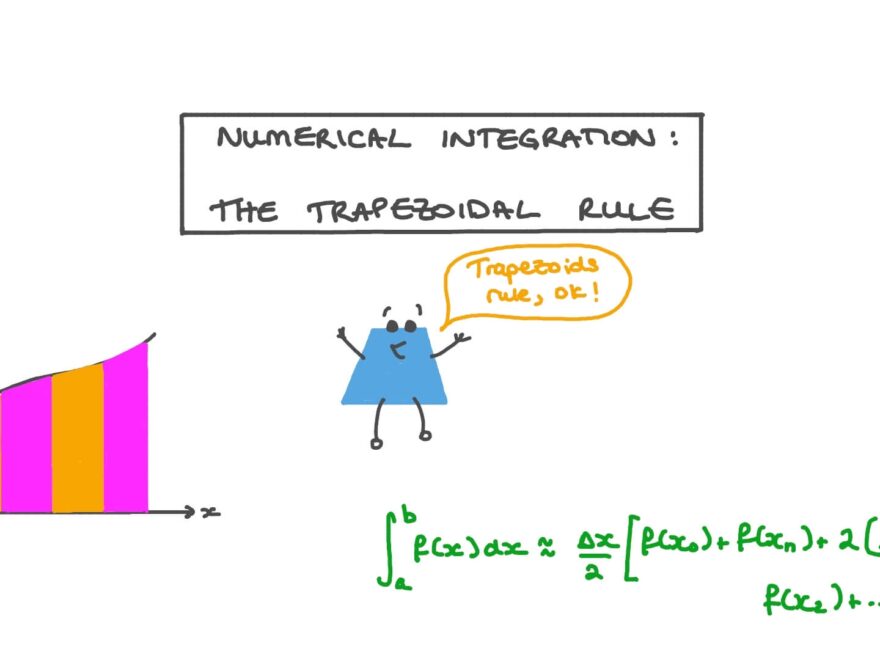
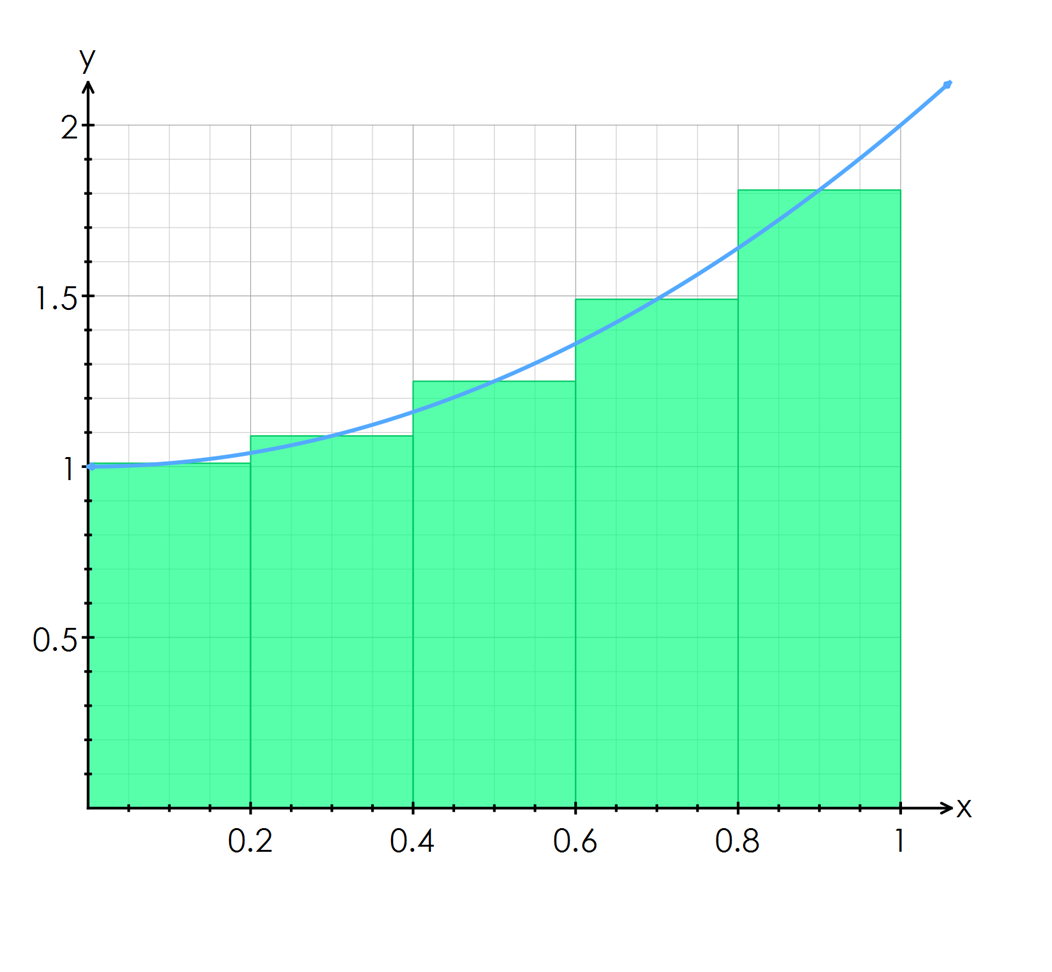
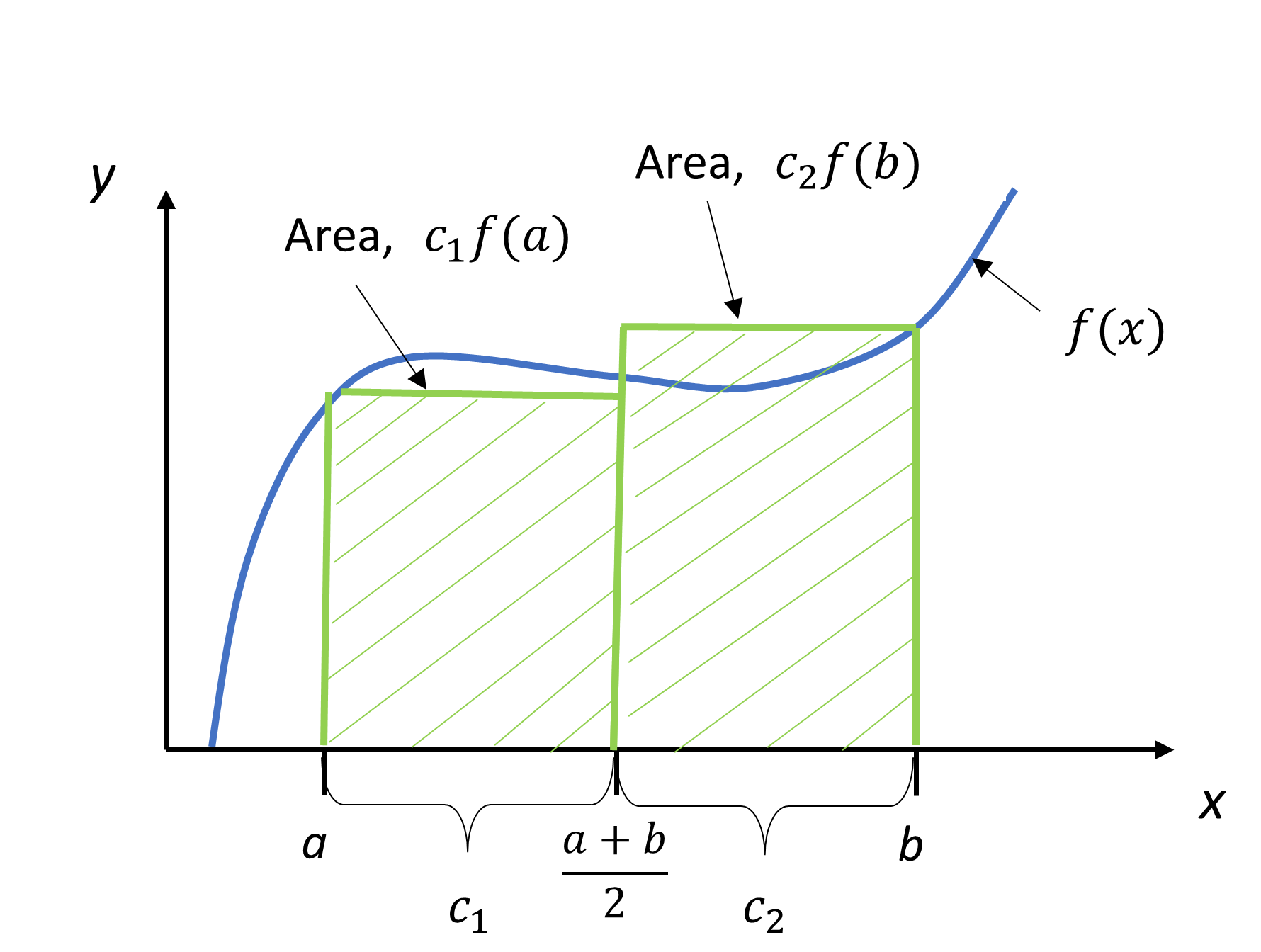
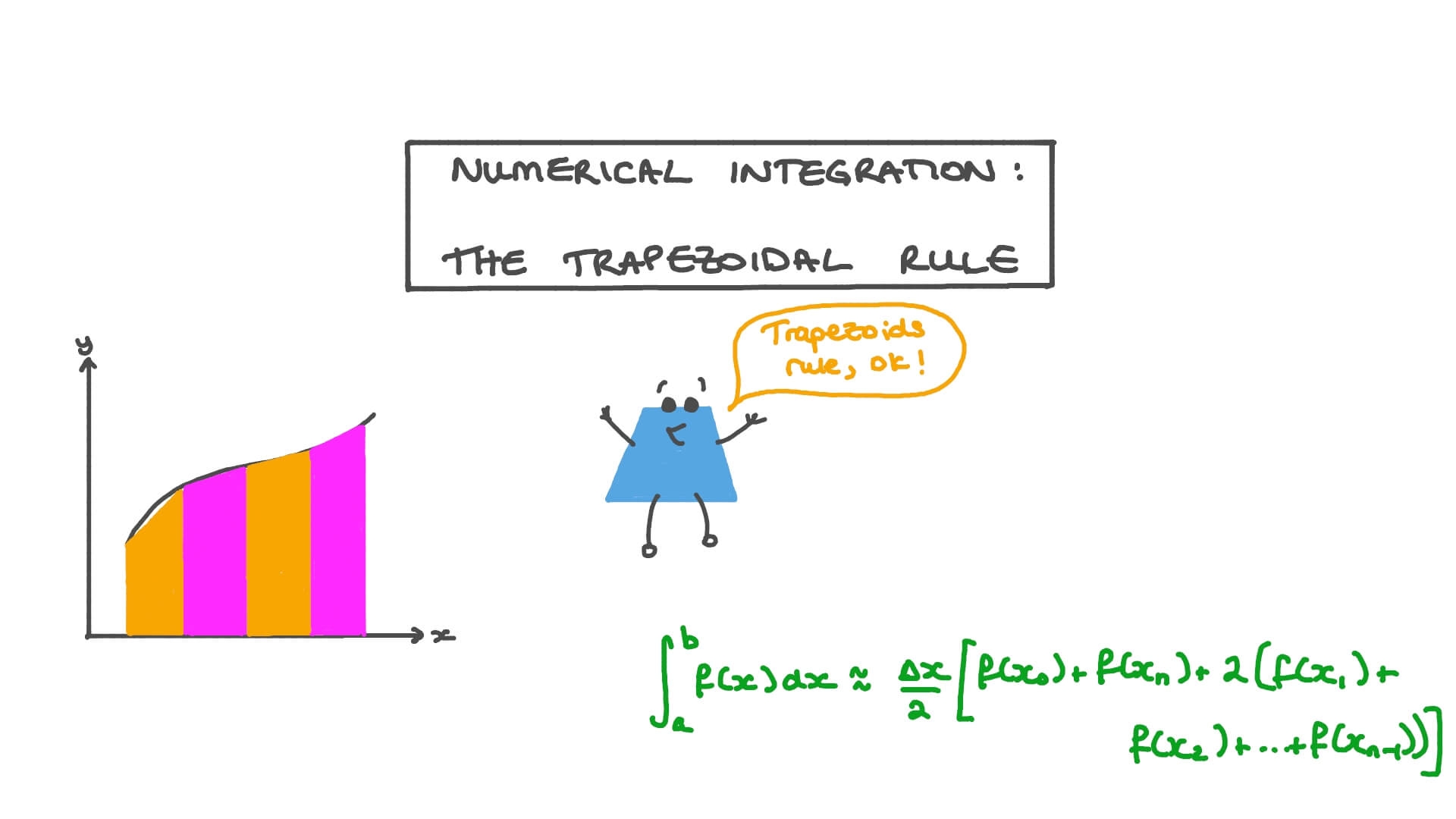
Math can be intimidating, but don’t worry! Today, we’re going to talk about the Trapezoidal Rule without needing a graph. This method makes approximating areas under curves much easier.
Instead of plotting points on a graph, the Trapezoidal Rule breaks up the area under a curve into trapezoids. By adding up the areas of these trapezoids, we can get a close estimate of the actual area.
Trapezoidal Rule Without A Graph
Trapezoidal Rule Without A Graph
To use the Trapezoidal Rule without a graph, you need to know the function you’re working with and the interval over which you want to approximate the area. Divide the interval into equal segments and calculate the height of each trapezoid.
Next, calculate the area of each trapezoid using the formula: A = 0.5 * (base1 + base2) * height. Add up the areas of all the trapezoids to get an estimate of the total area under the curve.
Keep in mind that the more trapezoids you use, the more accurate your approximation will be. However, using too many trapezoids can be time-consuming, so finding a balance is key.
By using the Trapezoidal Rule without a graph, you can quickly and easily approximate areas under curves without the need for complex graphing tools. This method is a handy tool for anyone studying calculus or needing to estimate areas in real-world scenarios.
So, next time you’re faced with a tricky area under a curve problem, remember the Trapezoidal Rule without a graph. With a bit of practice, you’ll be approximating areas like a pro in no time!
Chapter 07 02 Trapezoidal Rule Of Integration Numerical Methods With Applications
Lesson Video Numerical Integration The Trapezoidal Rule Nagwa