Mathematics can be intimidating, but fear not! Today, we’re going to break down the trapezoidal rule formula with a helpful graph to make it easier to understand.
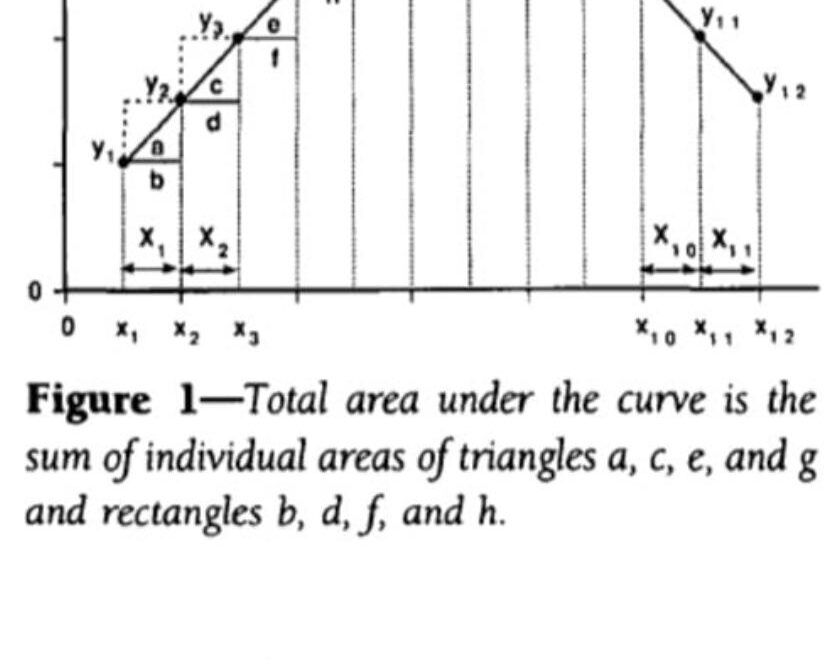
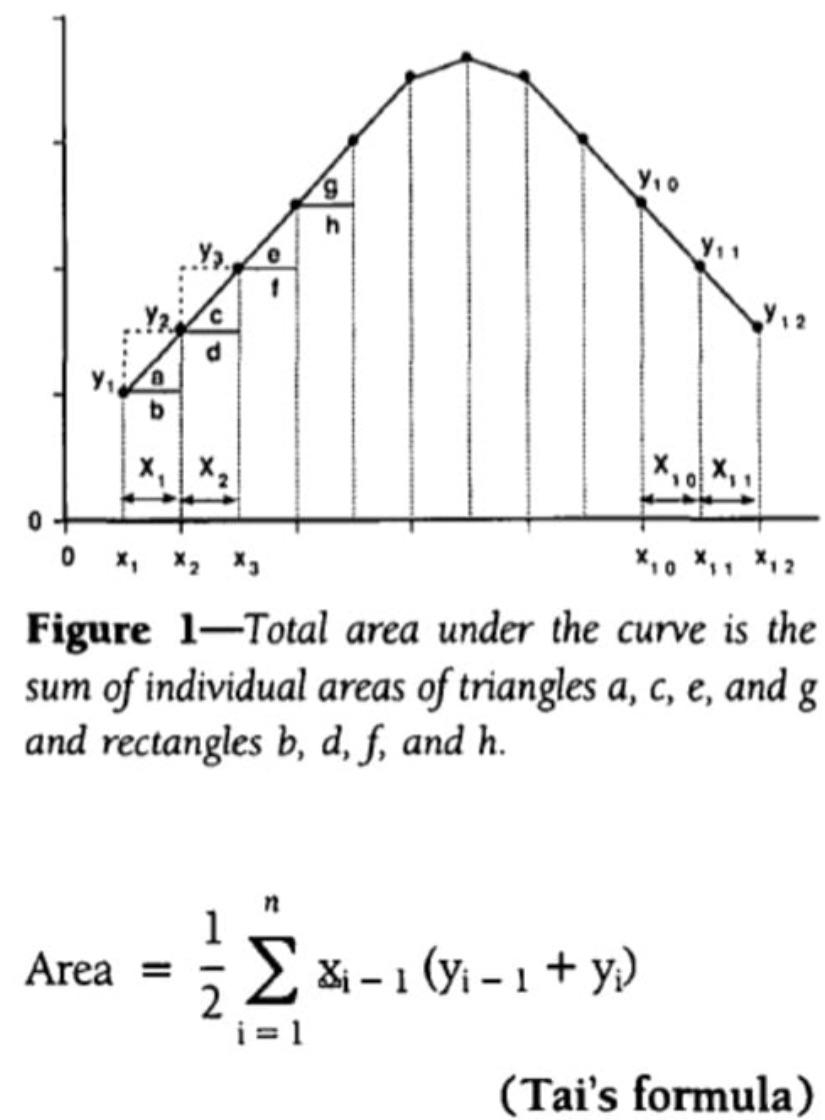
The trapezoidal rule is a method used in calculus to estimate the value of a definite integral. It involves approximating the area under a curve by dividing it into trapezoids.
Trapezoidal Rule Formula With Graph
Trapezoidal Rule Formula With Graph
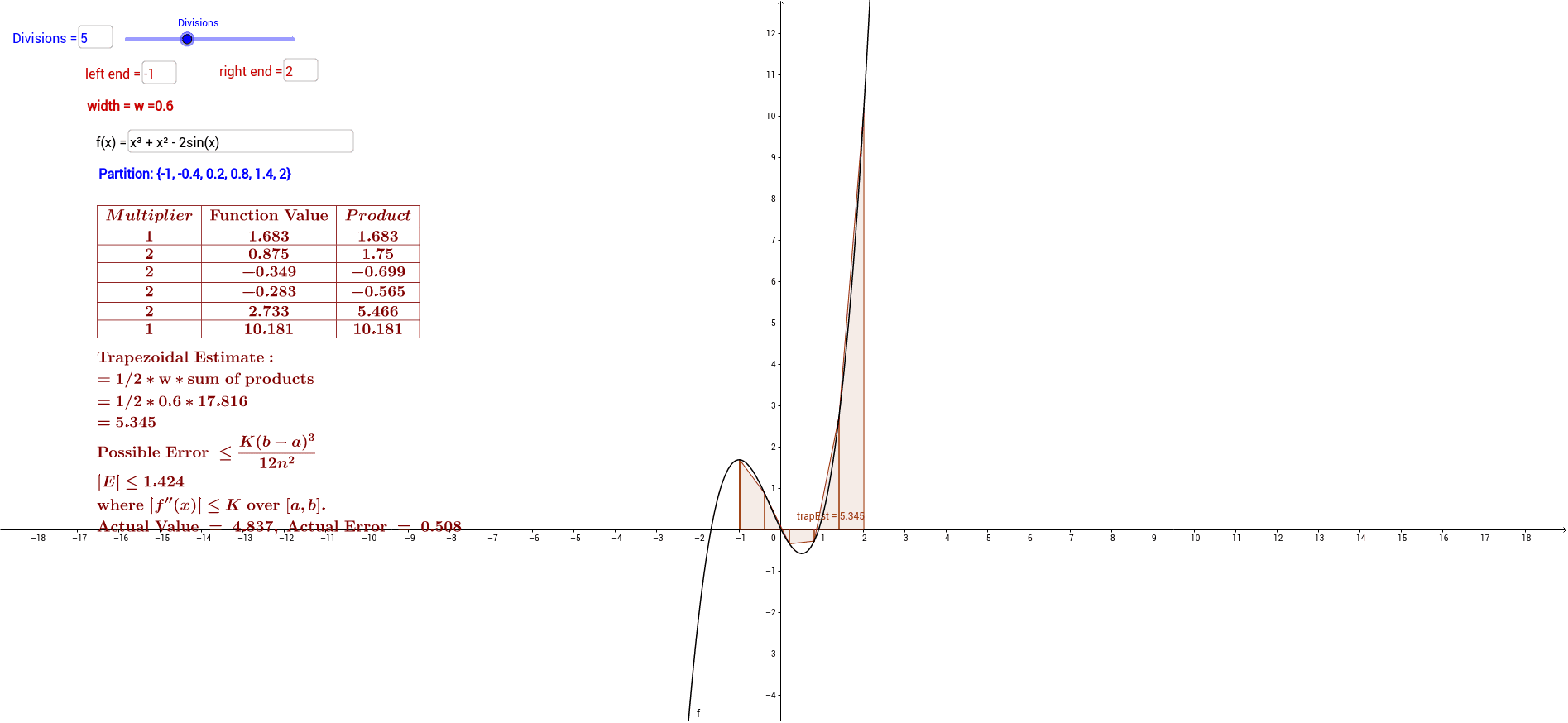
Let’s dive into the formula for the trapezoidal rule. Given a function f(x), the formula can be written as h/2 * (f(x0) + 2 * Σf(xi) + f(xn)). Here, h represents the width of each interval, and n is the number of intervals.
To better visualize how the trapezoidal rule works, let’s take a look at a graph. The graph will show the function f(x), the trapezoids created under the curve, and how the area of each trapezoid contributes to the overall estimate of the integral.
By using the trapezoidal rule formula and studying the corresponding graph, you can gain a deeper understanding of how to approximate definite integrals. Practice with different functions and intervals to sharpen your skills and grasp the concept more effectively.
In conclusion, the trapezoidal rule formula, coupled with a visual representation through a graph, is a valuable tool in calculus for estimating definite integrals. Embrace the challenge, practice regularly, and soon you’ll be a pro at using the trapezoidal rule to solve complex mathematical problems!
Question Video Integrating Functions Numerically Trapezoidal Rule Nagwa
This One Seems Familiar R mathmemes