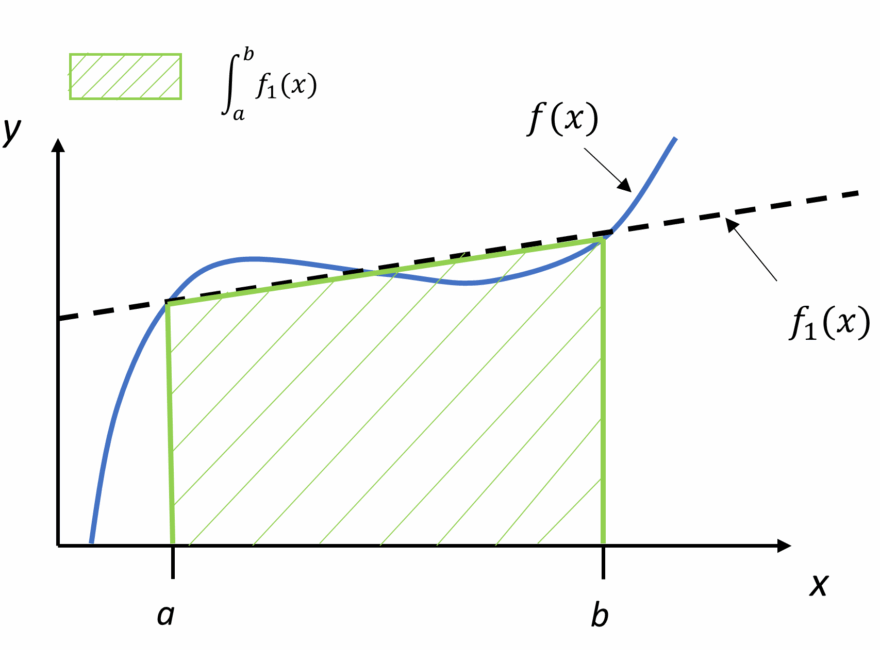
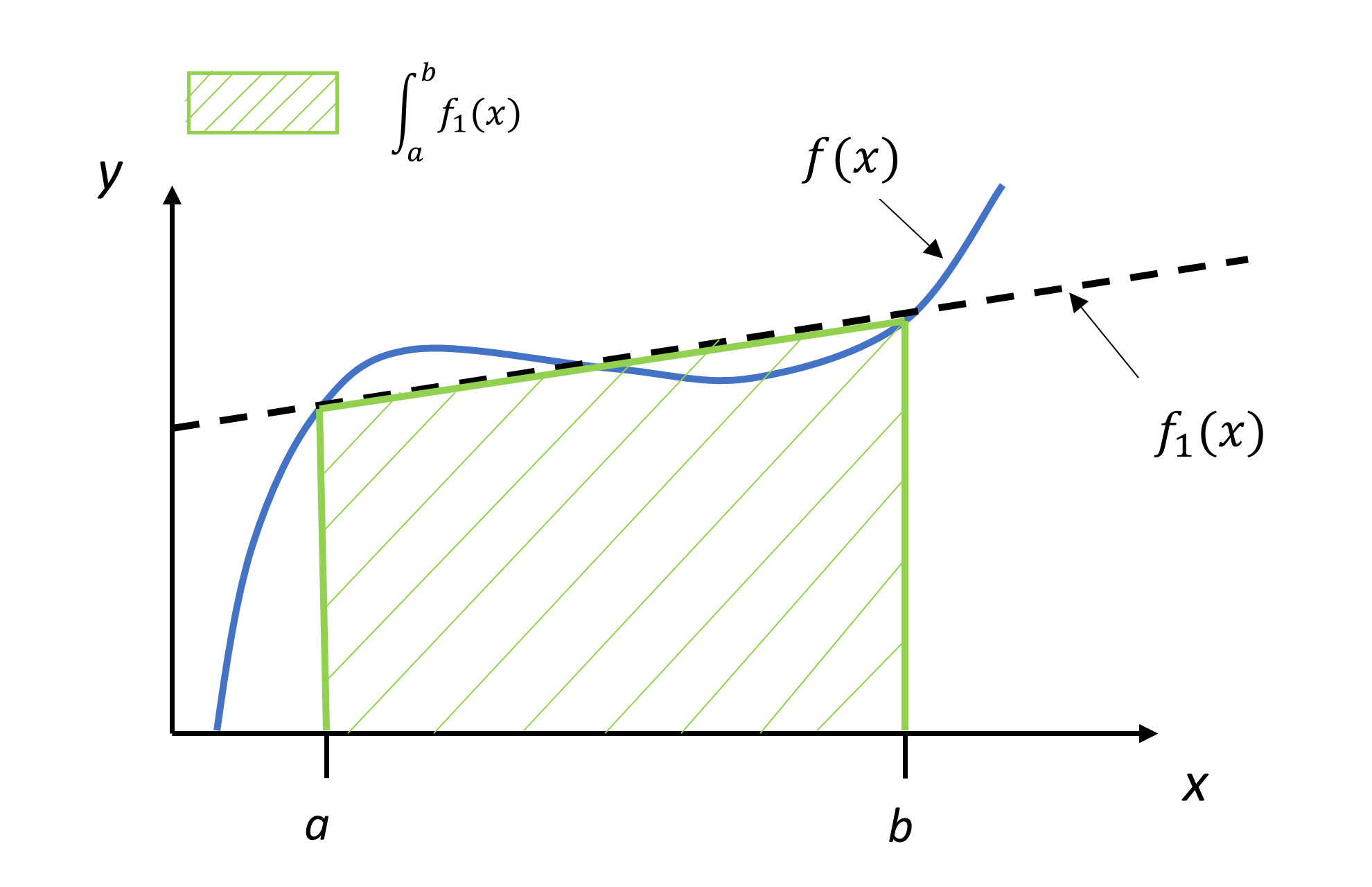
When it comes to finding the area under a curve or estimating definite integrals, the trapezoidal rule is a handy method that anyone studying calculus should know about. It’s a simple yet effective way to approximate the area under a curve by dividing it into trapezoids.
By using the trapezoidal rule, you can easily estimate the value of a definite integral by approximating the area under the curve using trapezoids instead of rectangles. This method is especially useful when you don’t have a straightforward formula to find the exact value of an integral.
Trapezoidal Rule For Points On A Graph
Trapezoidal Rule For Points On A Graph
To apply the trapezoidal rule, you first need to have a set of points on a graph that represent the function you want to find the area under. These points should be evenly spaced along the x-axis to ensure accurate results when approximating the area under the curve.
Once you have your points, you can calculate the area under the curve by summing up the areas of the trapezoids formed by connecting the points on the graph. The more points you have and the smaller the intervals between them, the more accurate your estimation will be.
Remember that the trapezoidal rule is an approximation method, so it won’t give you the exact value of the integral. However, it’s a quick and easy way to get a good estimate of the area under a curve without having to resort to more complex methods.
So next time you’re faced with estimating the area under a curve or finding the value of a definite integral, don’t forget about the trusty trapezoidal rule. It may not be perfect, but it’s a valuable tool to have in your calculus toolkit.
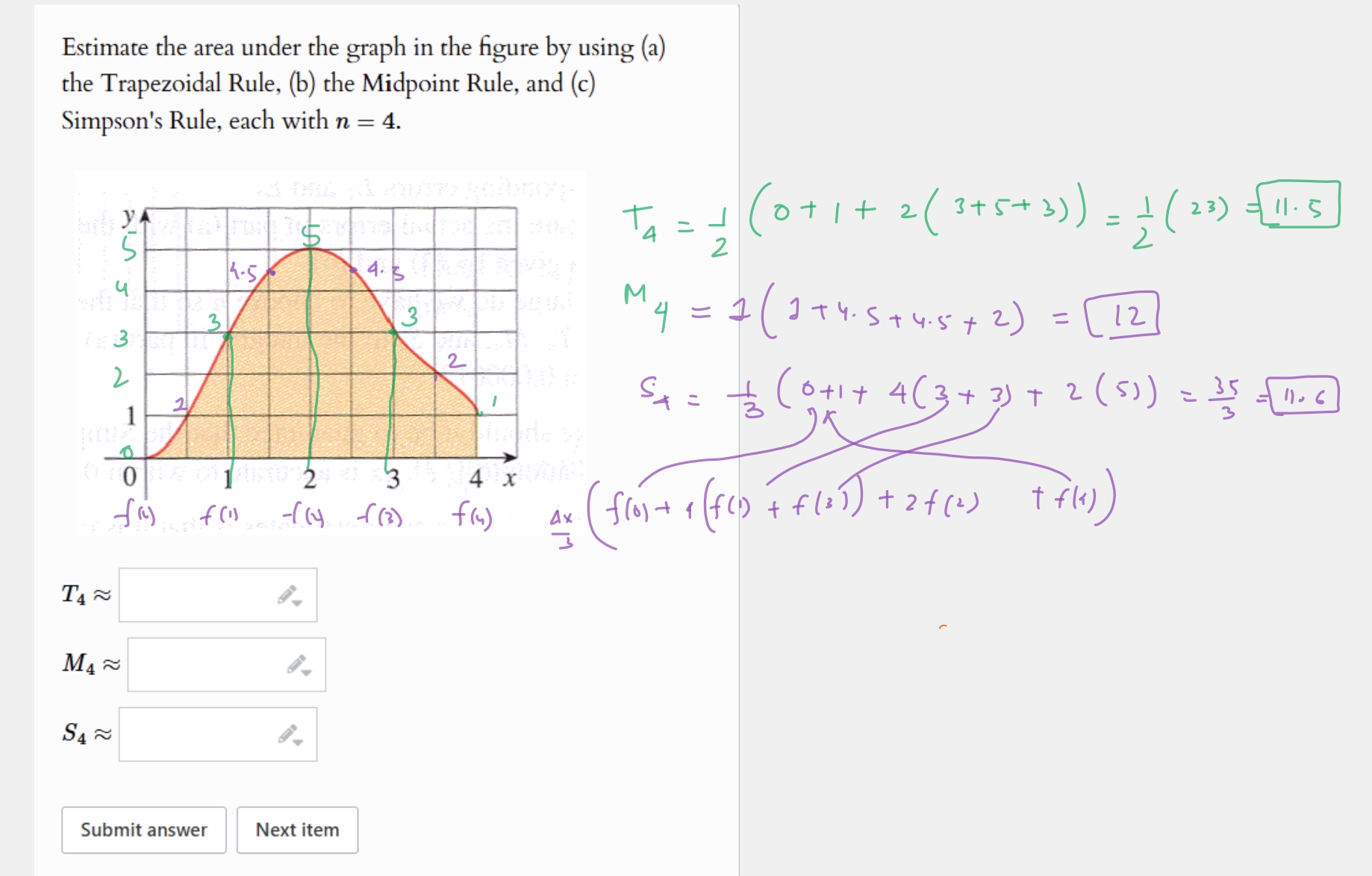
Area Under Graph Using Trapezoidal Mid Point And Simpson Rule Sumant s 1 Page Of Math
Chapter 07 02 Trapezoidal Rule Of Integration Numerical Methods With Applications