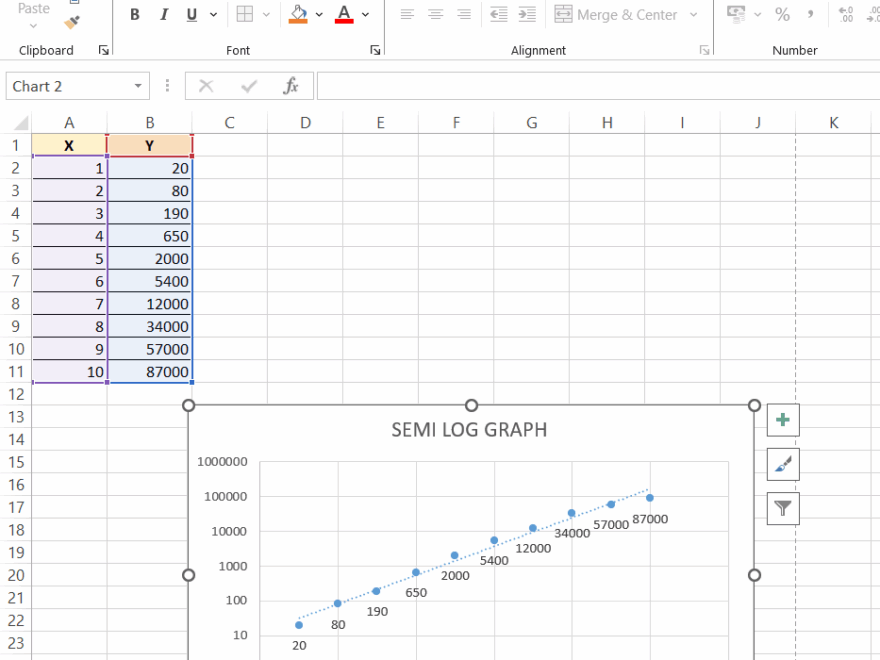
Understanding the slope formula for a semi-log graph is essential for anyone studying mathematics or science. This formula helps determine the rate of change or gradient on a graph that has one axis on a logarithmic scale.
When dealing with semi-log graphs, the x-axis is typically linear, while the y-axis is logarithmic. The slope of a line on a semi-log graph represents the exponential growth or decay of a variable, making it a powerful tool for analyzing data.
Slope Formula For Semi Log Graph
Slope Formula For Semi Log Graph
To calculate the slope on a semi-log graph, you need to find the change in the logarithmic value of y (Δlog(y)) divided by the change in x. The formula for slope on a semi-log graph is: Slope = Δlog(y) / Δx.
For example, if the log value of y changes by 2 units when x changes by 1 unit, the slope would be 2/1 = 2. This indicates that y is growing exponentially at a rate of 2 for every unit change in x.
By understanding the slope formula for a semi-log graph, you can analyze data more effectively and make predictions based on the rate of change. This knowledge is particularly valuable in fields such as biology, chemistry, economics, and engineering.
Practice calculating slopes on semi-log graphs with different datasets to strengthen your understanding of how variables are related and how they change over time. The more you work with this formula, the more confident you will become in interpreting graphs and drawing meaningful conclusions from your data.
In conclusion, mastering the slope formula for a semi-log graph is a valuable skill that can enhance your analytical abilities and problem-solving capabilities. By applying this formula to real-world data, you can uncover patterns, trends, and relationships that may not be immediately apparent. Keep practicing and exploring the world of semi-log graphs to deepen your understanding and excel in your studies or professional endeavors.
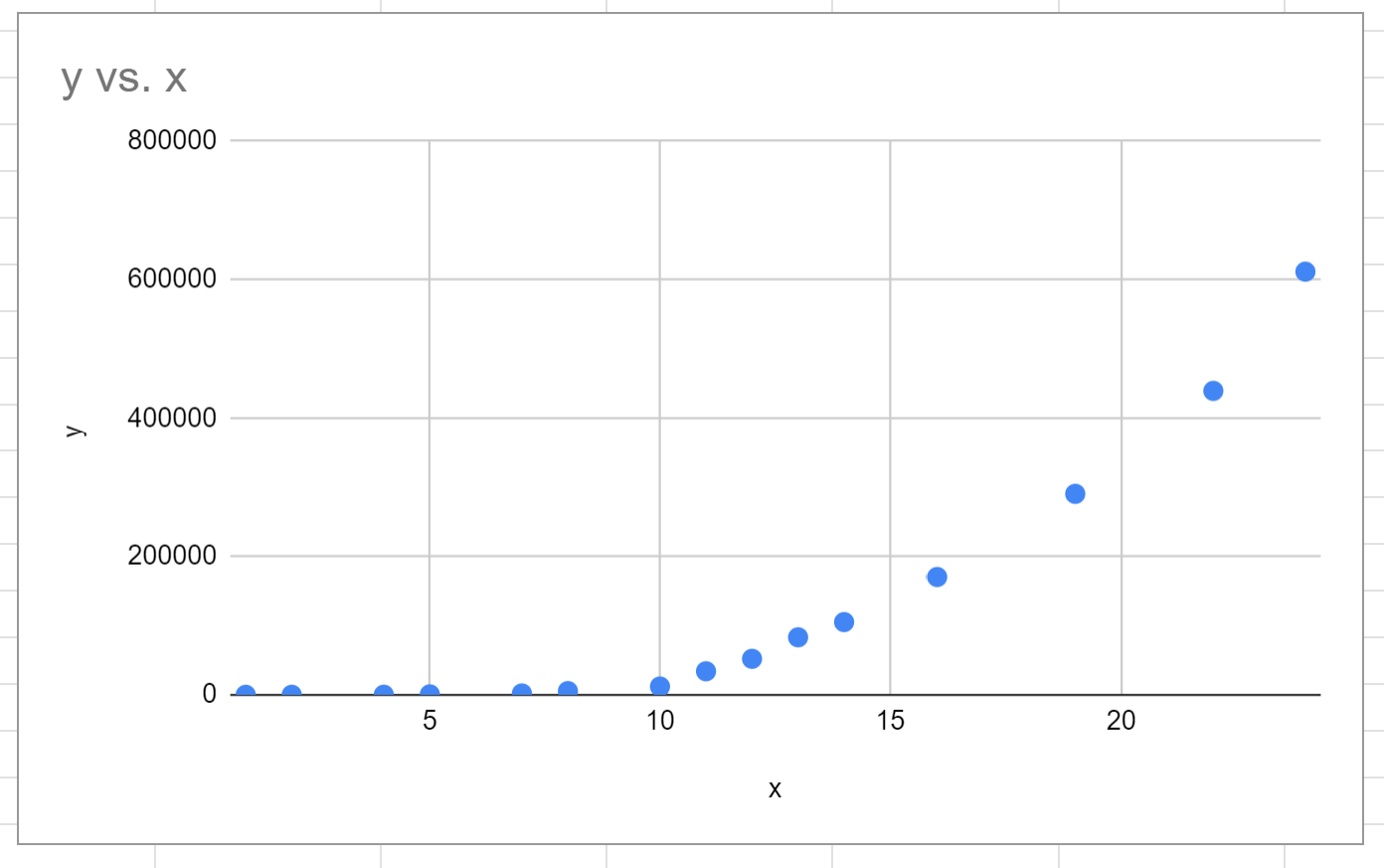
How To Create A Semi Log Graph In Google Sheets
Semi Log Graph In Excel How To Create Precise Charts Fast MyExcelOnline