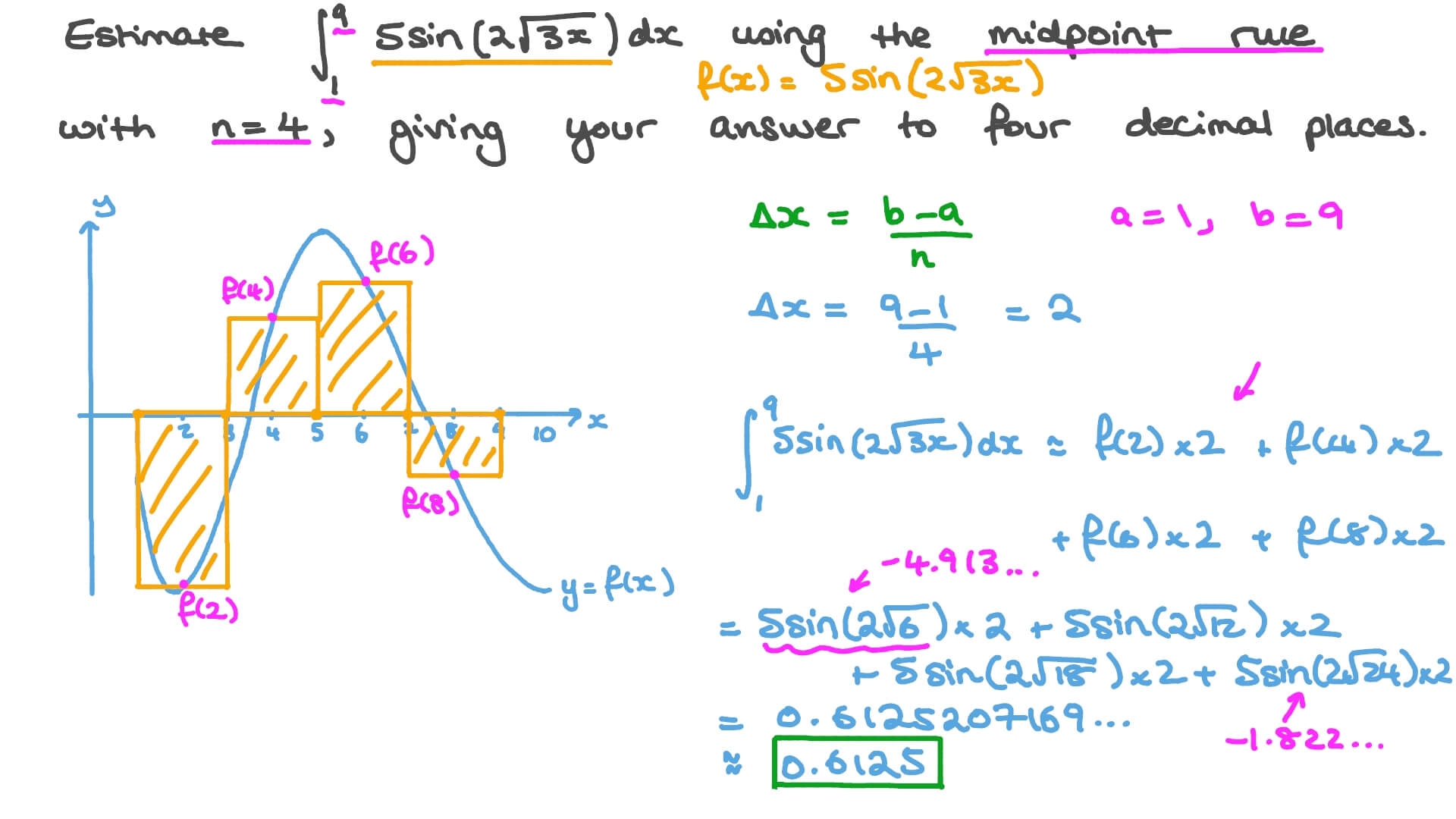
Have you ever heard of the Midpoint Rule on a graph? It’s a handy tool used in calculus to approximate the area under a curve. By dividing the area into rectangles and finding their midpoints, you can get a good estimate of the total area.
Understanding the Midpoint Rule can help you solve complex integration problems with ease. It’s a great way to get a rough idea of the total area under a curve without having to go through the tedious process of calculating exact values.
Midpoint Rule On Graph
Midpoint Rule On Graph
When using the Midpoint Rule, you divide the area under a curve into smaller rectangles and find the midpoint of each one. Then, you calculate the area of each rectangle using the height of the curve at the midpoint. Finally, you sum up the areas of all the rectangles to get an approximation of the total area.
While the Midpoint Rule may not give you the exact area under a curve, it provides a good estimate, especially when dealing with curves that are difficult to integrate directly. It’s a valuable tool for engineers, scientists, and mathematicians who need quick and reliable approximations in their work.
By visualizing the rectangles and midpoints on a graph, you can see how the Midpoint Rule works in action. It’s a hands-on approach to understanding integration and can help you grasp the concept more intuitively than just working with equations and formulas.
Next time you encounter a challenging integration problem, consider using the Midpoint Rule on a graph to simplify your calculations. It’s a practical technique that can save you time and effort while still providing accurate results. Give it a try and see how it can enhance your problem-solving skills!
Exploring the Midpoint Rule on a graph opens up a new perspective on calculus and integration. By breaking down complex curves into simpler components, you can tackle challenging problems with confidence and efficiency. So, dive into the world of the Midpoint Rule and unleash your potential in mathematical analysis!
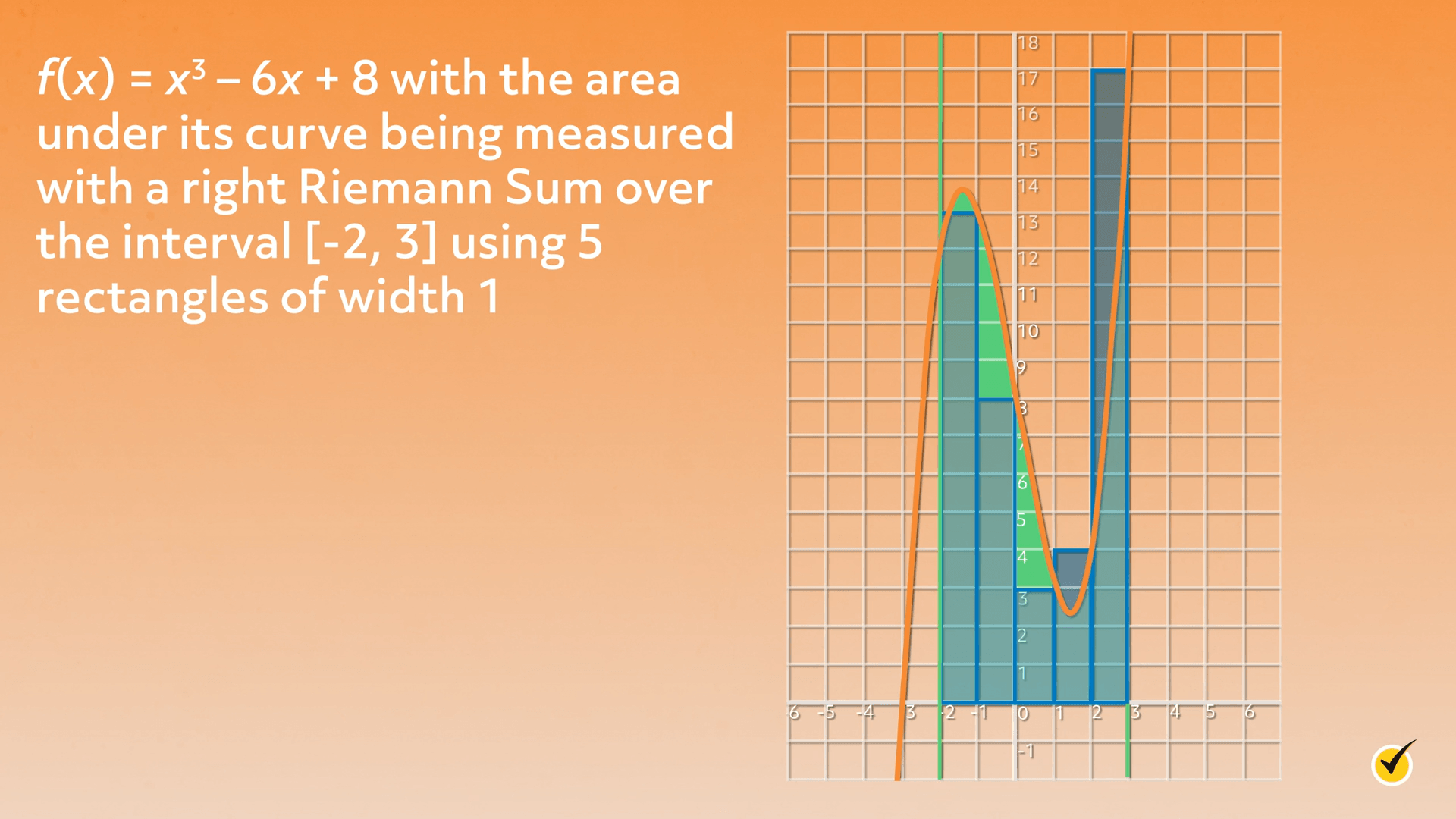
The Midpoint Rule And The Riemann Sum Video
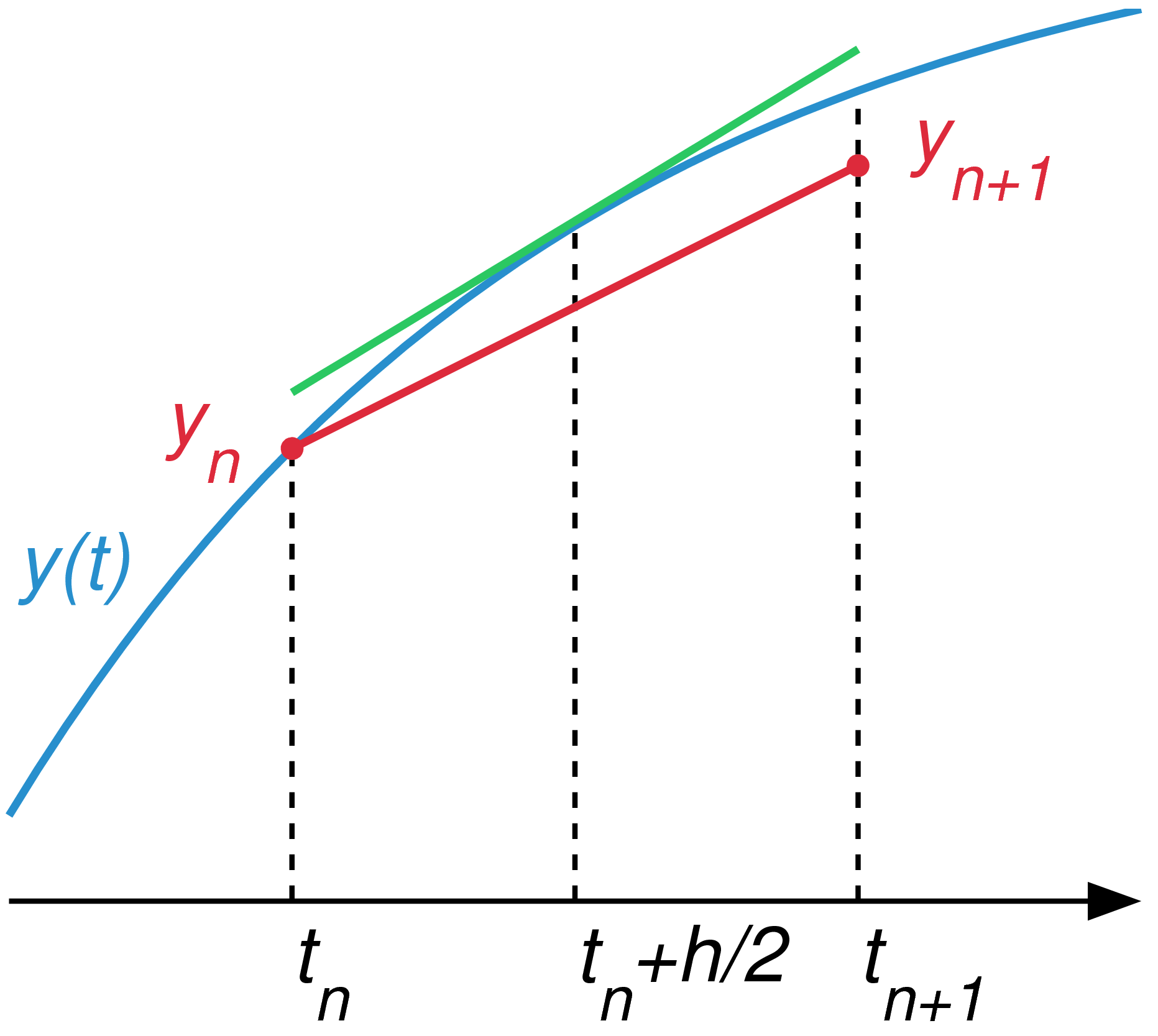
Midpoint Method Wikipedia