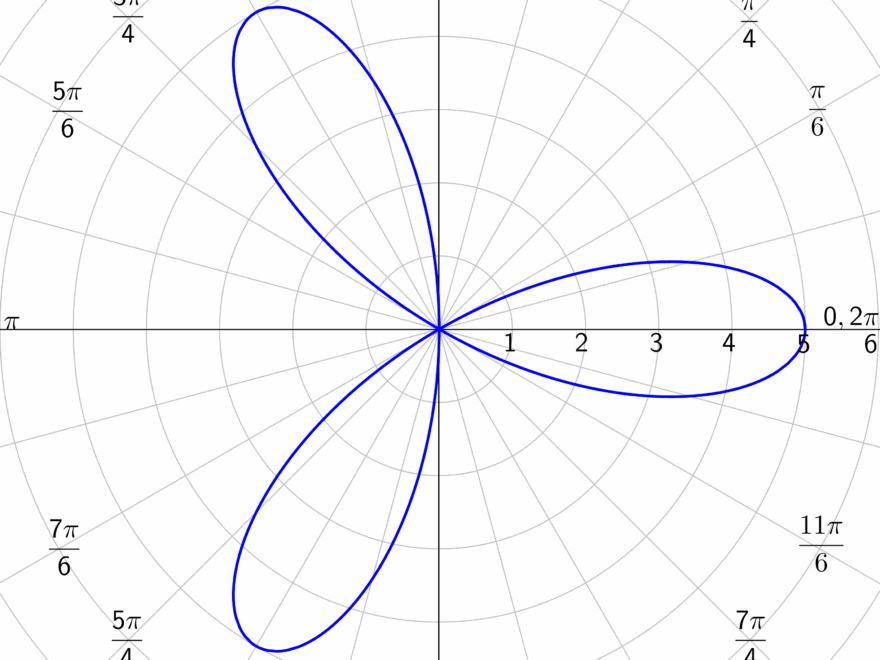
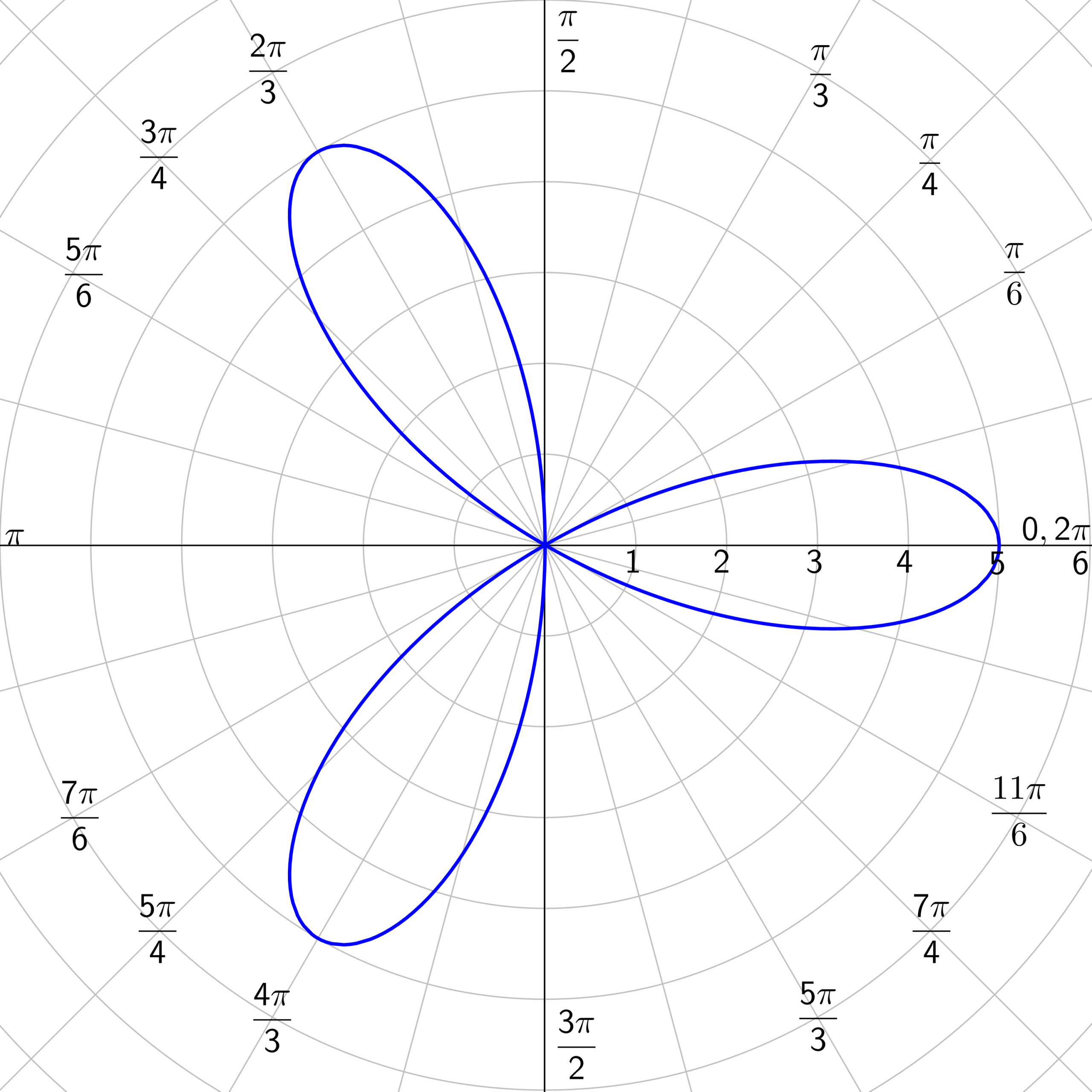
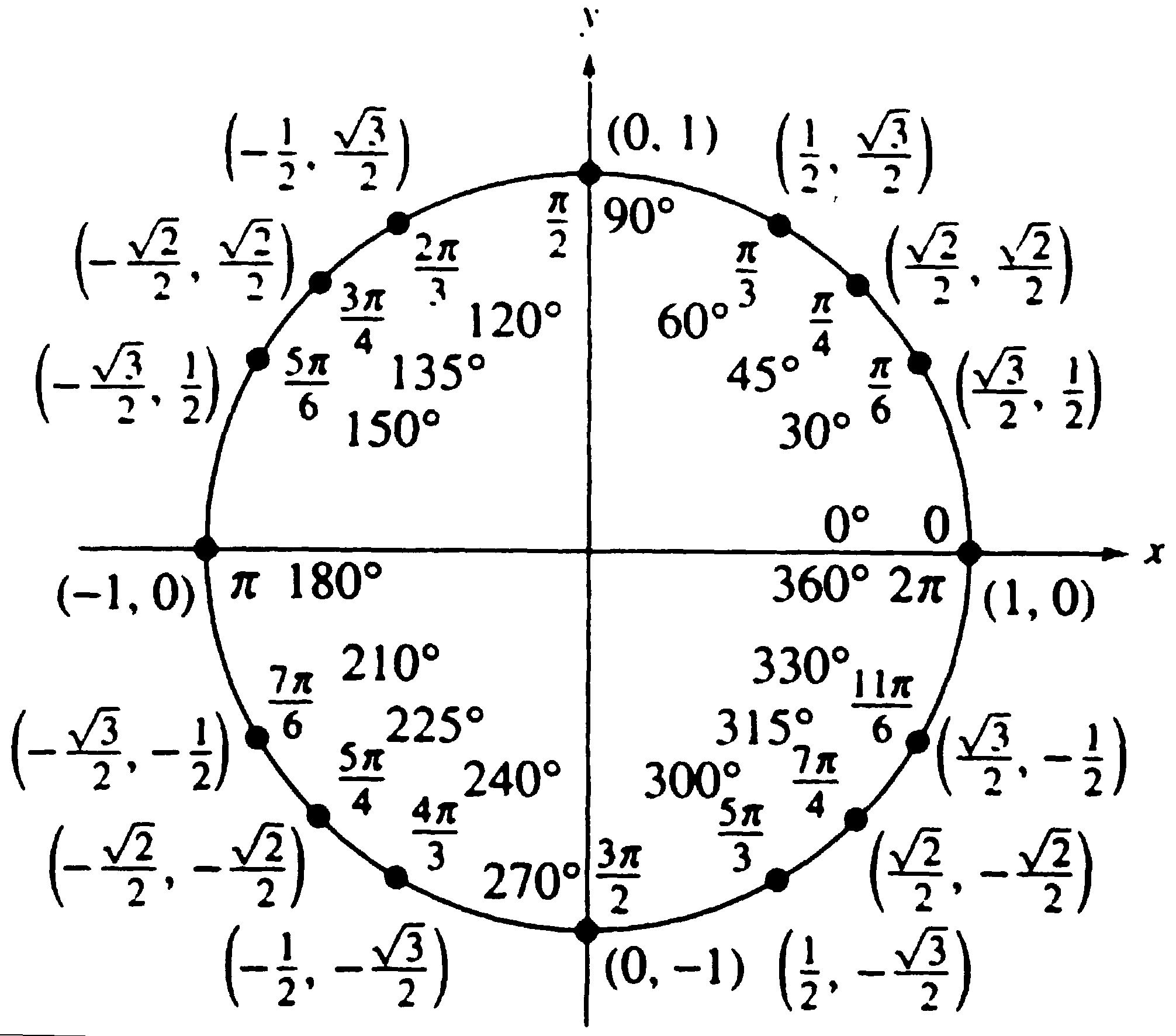Have you ever wondered how the graph of a sine function looks like when plotted in polar coordinates? It’s a fascinating concept that combines trigonometry and geometry in a unique way.
When we think of a sine wave, we usually visualize it as a curve oscillating up and down on a Cartesian plane. But when we switch to polar coordinates, things get a bit more interesting.
Graph Of Sine In Polar Coordinates
Graph Of Sine In Polar Coordinates
In polar coordinates, the graph of a sine function creates a beautiful spiral pattern. As the angle increases, the radius of the spiral changes, creating a mesmerizing visual representation of the sine wave.
By plotting the sine function in polar coordinates, we can explore how the amplitude and frequency of the wave affect the shape of the spiral. It’s a great way to understand the relationship between trigonometry and polar geometry.
One of the key advantages of representing the sine function in polar coordinates is that it allows us to visualize complex waveforms in a more intuitive manner. This can be especially helpful in fields such as physics, engineering, and astronomy.
Next time you’re studying trigonometry or exploring the beauty of mathematics, take a moment to dive into the world of polar coordinates and discover the mesmerizing graph of the sine function. It’s a unique perspective that will enhance your understanding of the mathematical universe.
So, the next time you come across the graph of a sine function in polar coordinates, take a moment to appreciate the intricate beauty of this mathematical concept. It’s a powerful reminder of the interconnectedness of different branches of mathematics and the endless possibilities they offer.
Cochranmath Equations For The Polar Graphs
7 08 Graphs Of Polar Equations