Have you ever wondered how to graph for polar coordinates works? Well, you’re in luck because we’re here to break it down for you in a simple and easy-to-understand way. Polar coordinates are a different way of representing points in the plane compared to the traditional Cartesian coordinates.
Instead of using x and y coordinates, polar coordinates use a radius (r) and an angle (θ) to pinpoint a location. The radius tells you how far away the point is from the origin, while the angle tells you in which direction the point is located.
Graph For Polar Coordinates
Graph For Polar Coordinates
To graph a point in polar coordinates, you first locate the angle θ on the polar axis (usually the positive x-axis) and then move r units away from the origin in that direction. This process creates a unique point in the plane that can be represented by its polar coordinates (r, θ).
When graphing curves in polar coordinates, things get a bit more interesting. For example, a line in polar coordinates is represented by an equation of the form r = a, where ‘a’ is a constant. This equation produces a circle centered at the origin with radius ‘a’.
Other common curves in polar coordinates include cardioids, limaçons, and spirals. Each of these curves has a unique equation that can be used to plot its shape on a polar graph. By understanding these equations and how they relate to the radius and angle, you can create beautiful and intricate designs on a polar graph.
In conclusion, graphing for polar coordinates may seem intimidating at first, but with a little practice and understanding of the basic concepts, you’ll be able to navigate the polar plane with ease. So grab your pencil, paper, and some trigonometry knowledge, and start exploring the fascinating world of polar coordinates!
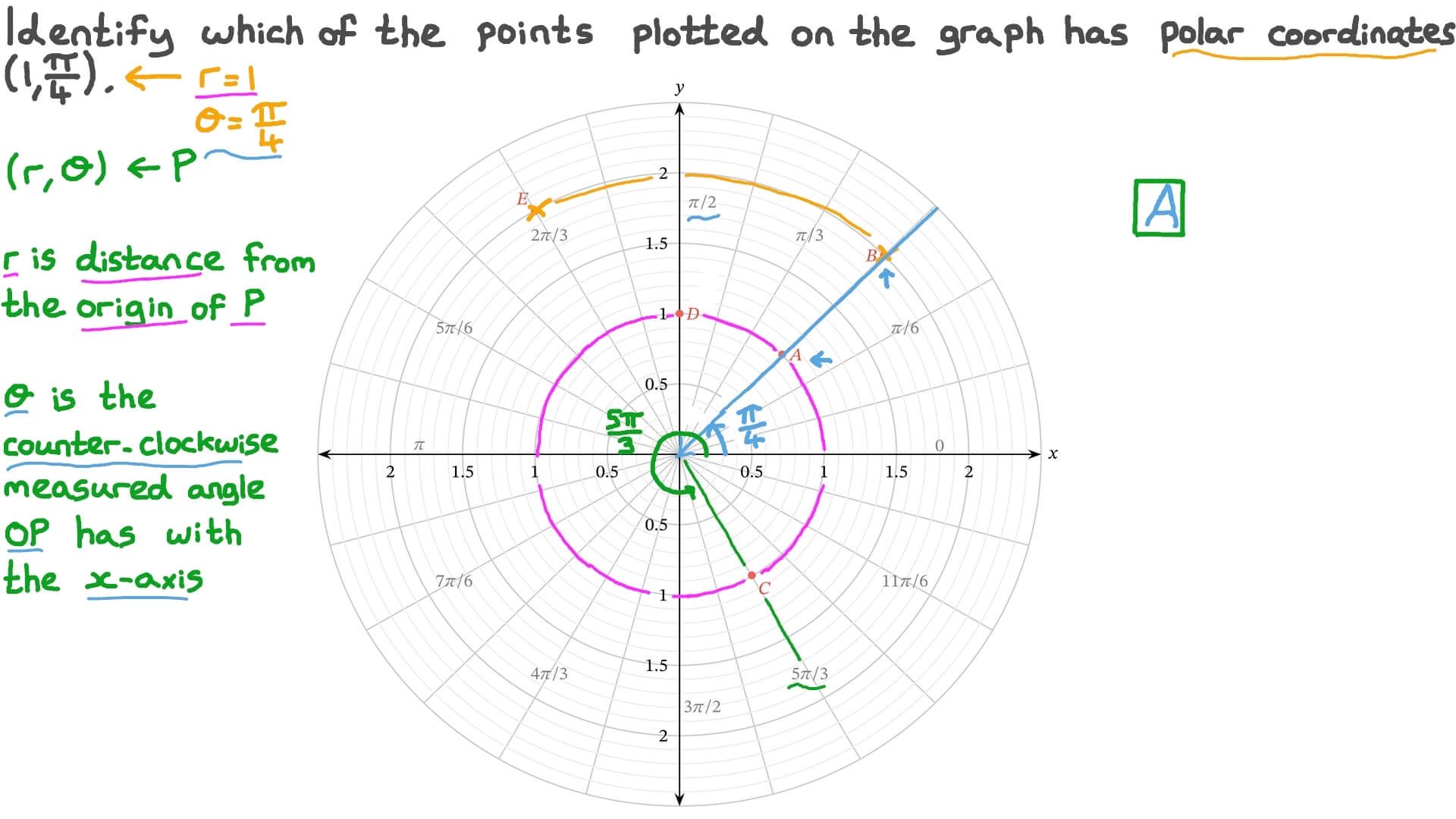
Question Video Graphing Polar Coordinates Nagwa
Polar Coordinates A Minimum Of Blind Calculation