Have you ever wondered what the term “curvature” means in the context of a graph in a Cartesian coordinate system? If so, you’re not alone! Understanding curvature can help us visualize the shape of a curve and how it changes at different points.
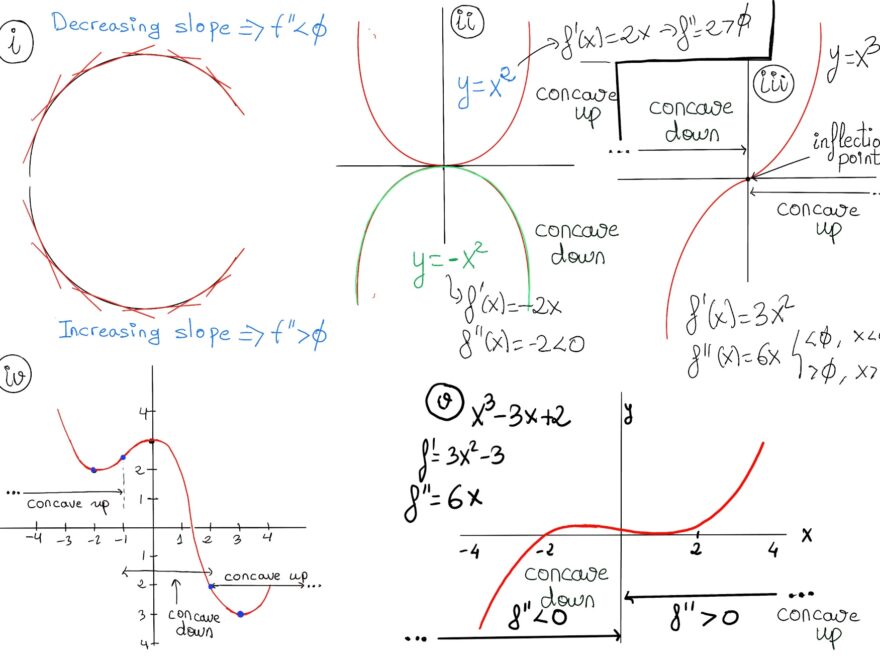
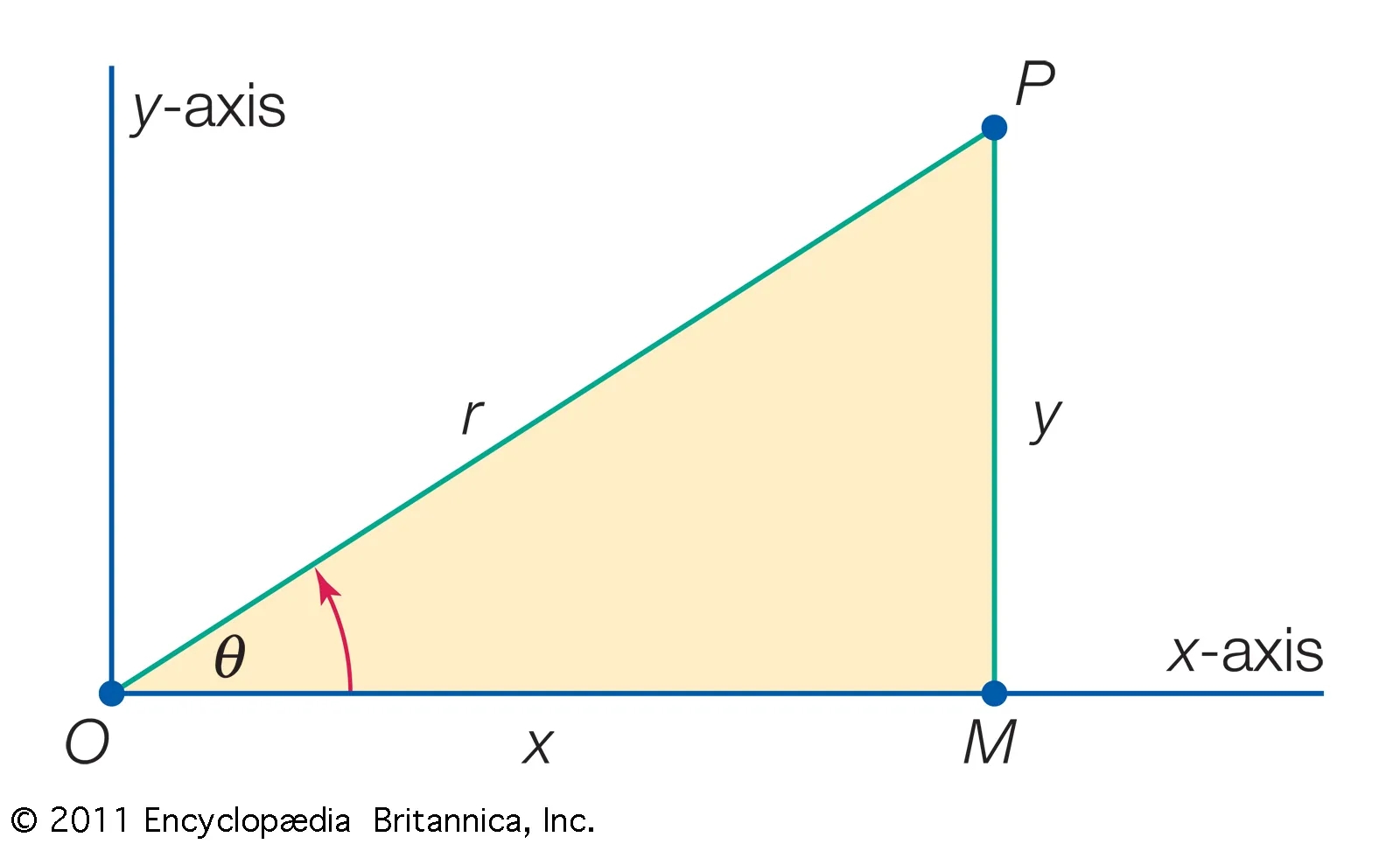
Curvature is a measure of how much a curve deviates from being a straight line. In a Cartesian coordinate system, it tells us how sharply a curve bends at a given point. The greater the curvature, the more the curve deviates from being a straight line.
Curvature Mean In Graph Cartesian Coordinate System
Curvature Mean In Graph Cartesian Coordinate System
When we calculate the curvature of a curve at a specific point, we are essentially measuring how fast the tangent direction of the curve is changing at that point. Think of it as a way to quantify how “curvy” a curve is at a particular location.
Curvature can be positive, negative, or zero, depending on the shape of the curve. A circle, for example, has a constant positive curvature, while a straight line has zero curvature. Curves with sharper bends will have higher curvature values.
By understanding curvature, we can gain insights into the behavior of a curve and its geometric properties. For example, in physics and engineering, curvature plays a crucial role in analyzing the trajectory of objects in motion and designing efficient paths for vehicles to follow.
Next time you look at a graph in a Cartesian coordinate system, take a moment to appreciate the concept of curvature and how it influences the shape of the curve. It’s a fascinating aspect of mathematics that helps us make sense of the world around us!
Fundamentals Of Data Visualization
Concavity And Inflection Points JustToThePoint