Are you struggling with converting Cartesian coordinates to polar coordinates on a graph? It can be a tricky concept to grasp, but with a little practice, you’ll be a pro in no time. Let’s break it down step by step.
Cartesian coordinates are the familiar (x, y) points on a graph, while polar coordinates use (r, θ) to represent a point’s distance from the origin and its angle. Converting between the two systems involves some simple trigonometry and geometry.
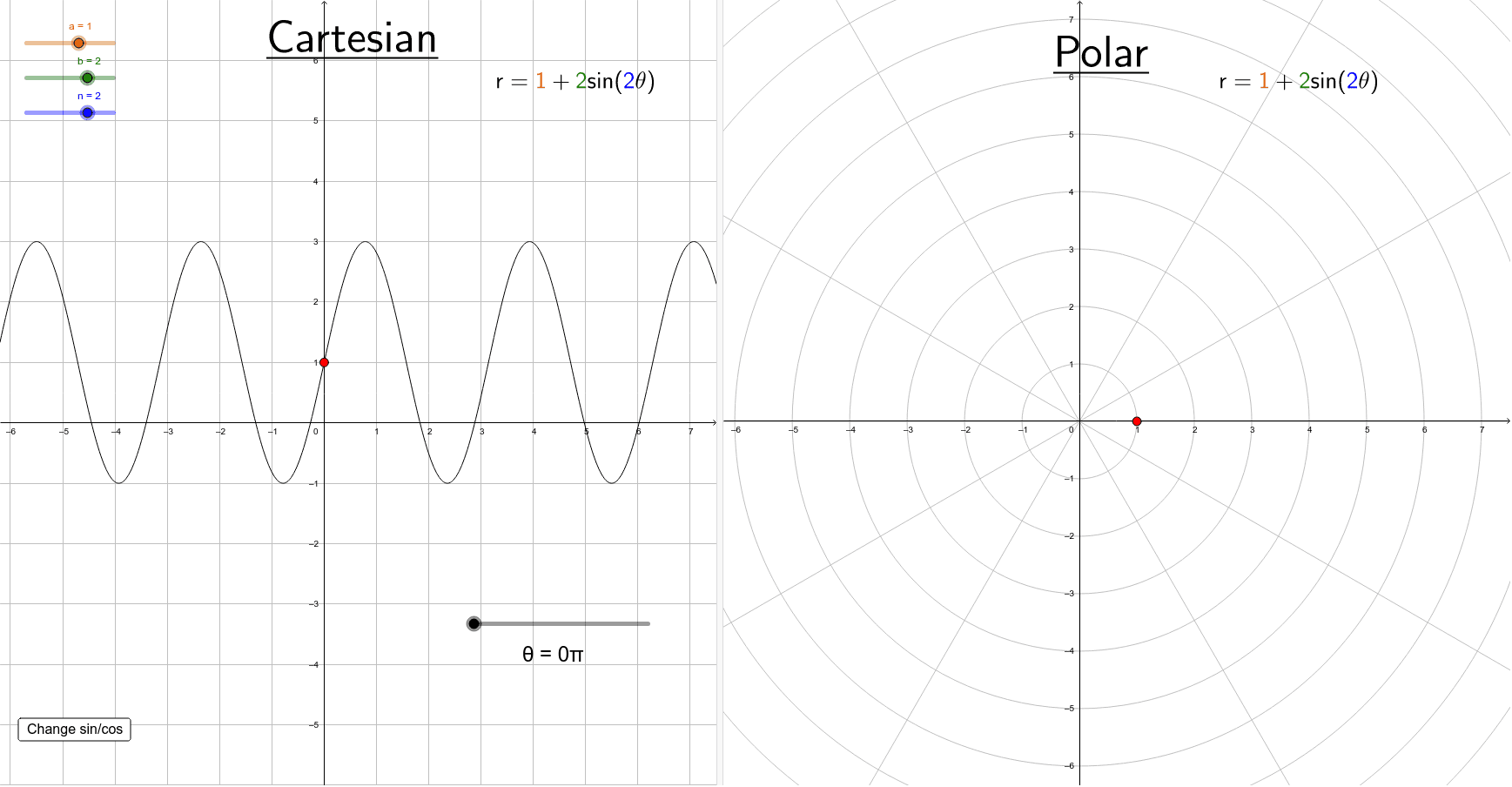
Cartesian Coordinates To Polar Coordinates Graph
Cartesian Coordinates To Polar Coordinates Graph
To convert Cartesian coordinates to polar coordinates, you can use the formulas r = sqrt(x^2 + y^2) and θ = arctan(y/x). Simply plug in your (x, y) values and calculate the corresponding (r, θ) coordinates. Remember that angles in polar coordinates are measured in radians.
For example, let’s say you have a point at (3, 4) in Cartesian coordinates. To convert this to polar coordinates, you would calculate r = sqrt(3^2 + 4^2) = 5 and θ = arctan(4/3) ≈ 0.93 radians. So, the point in polar coordinates would be (5, 0.93).
Understanding how to convert between Cartesian and polar coordinates is essential for many mathematical and scientific applications. It allows you to work with different coordinate systems and make complex calculations more manageable. So, take the time to practice and master this skill.
Next time you encounter a graph with polar coordinates, you’ll be able to navigate it with ease. Remember, practice makes perfect, so don’t get discouraged if it takes a few tries to get the hang of it. Keep at it, and soon you’ll be a pro at converting between Cartesian and polar coordinates on a graph.
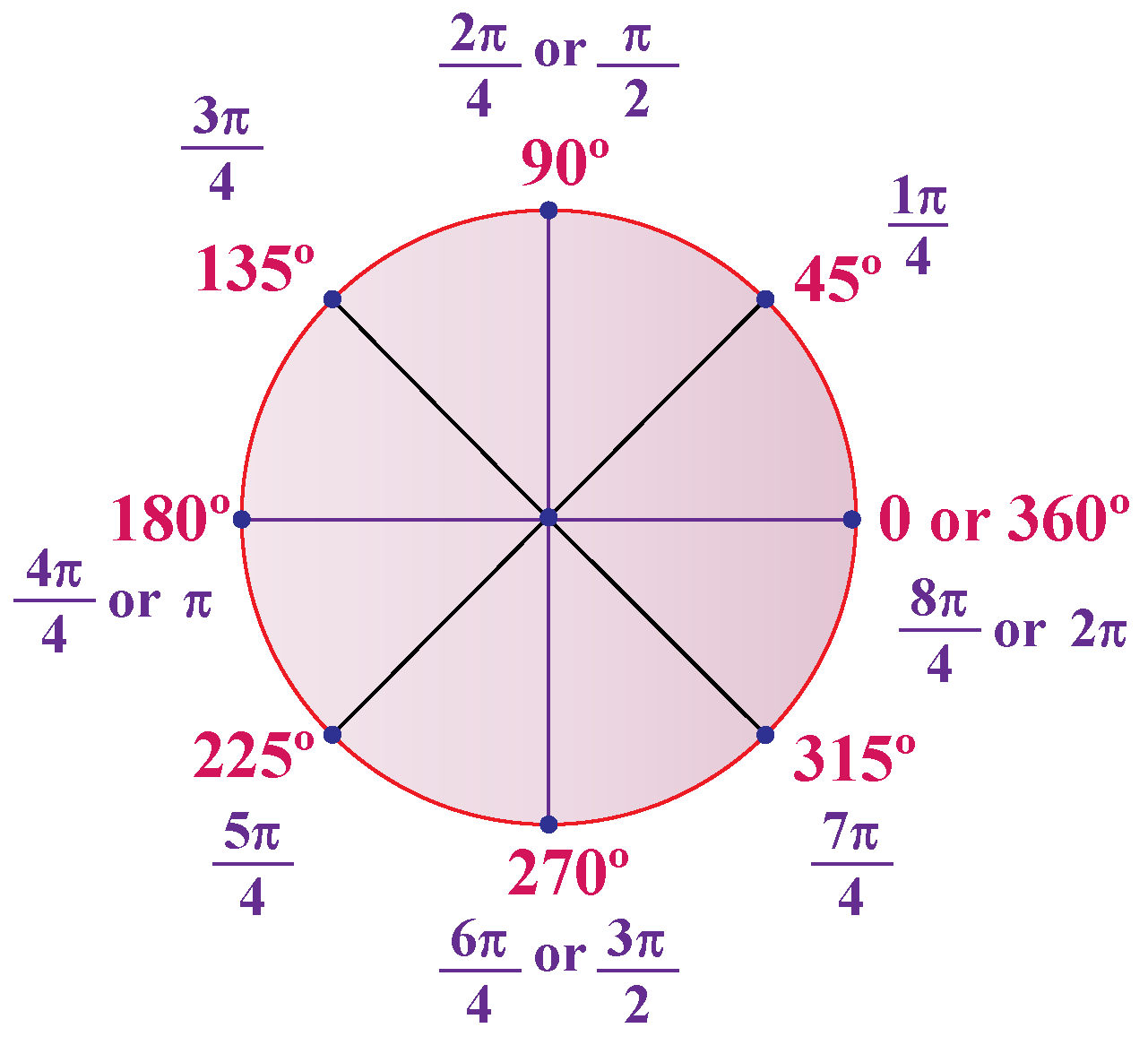
Polar Coordinates Cuemath
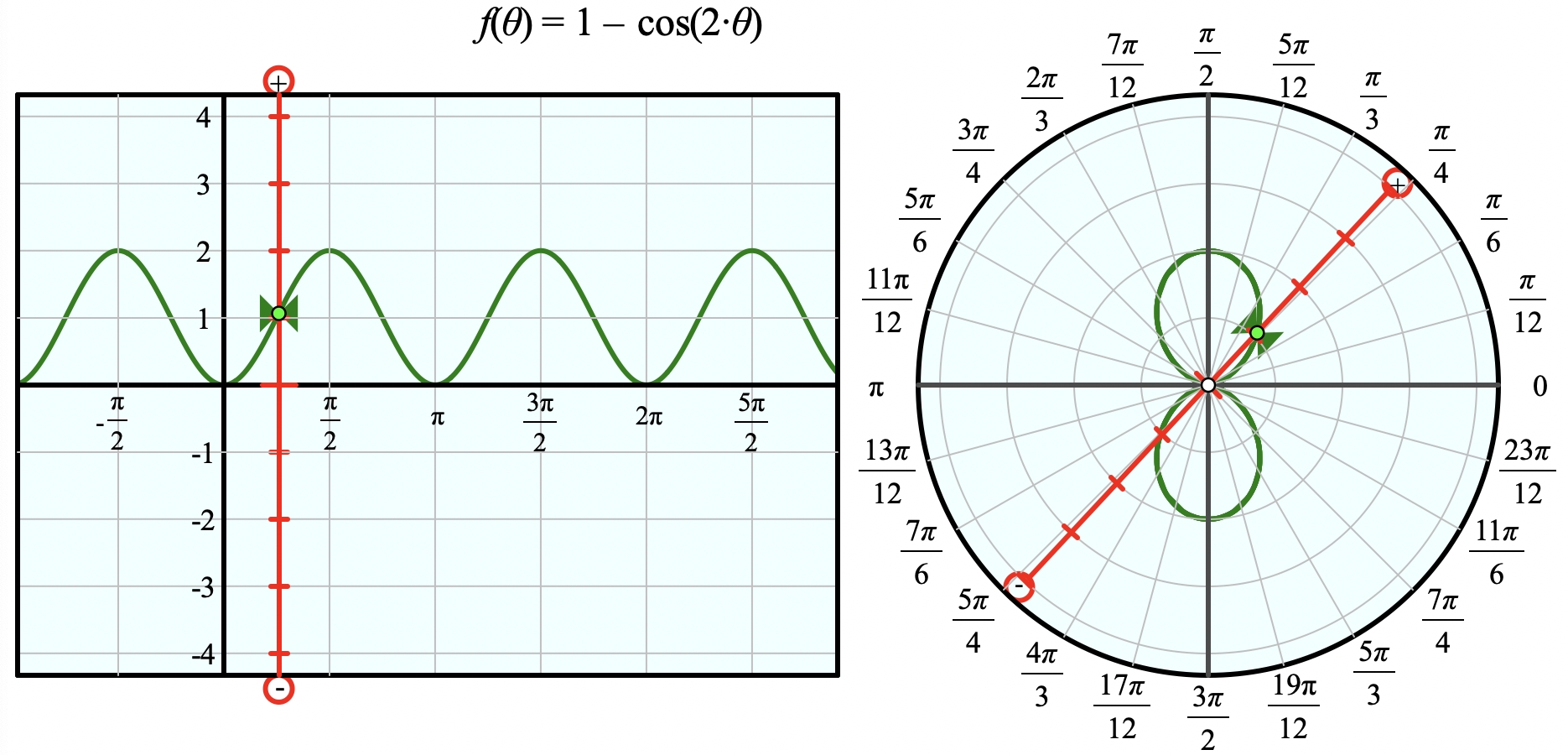
Cartesian And Polar Graphs Sine Of The Times