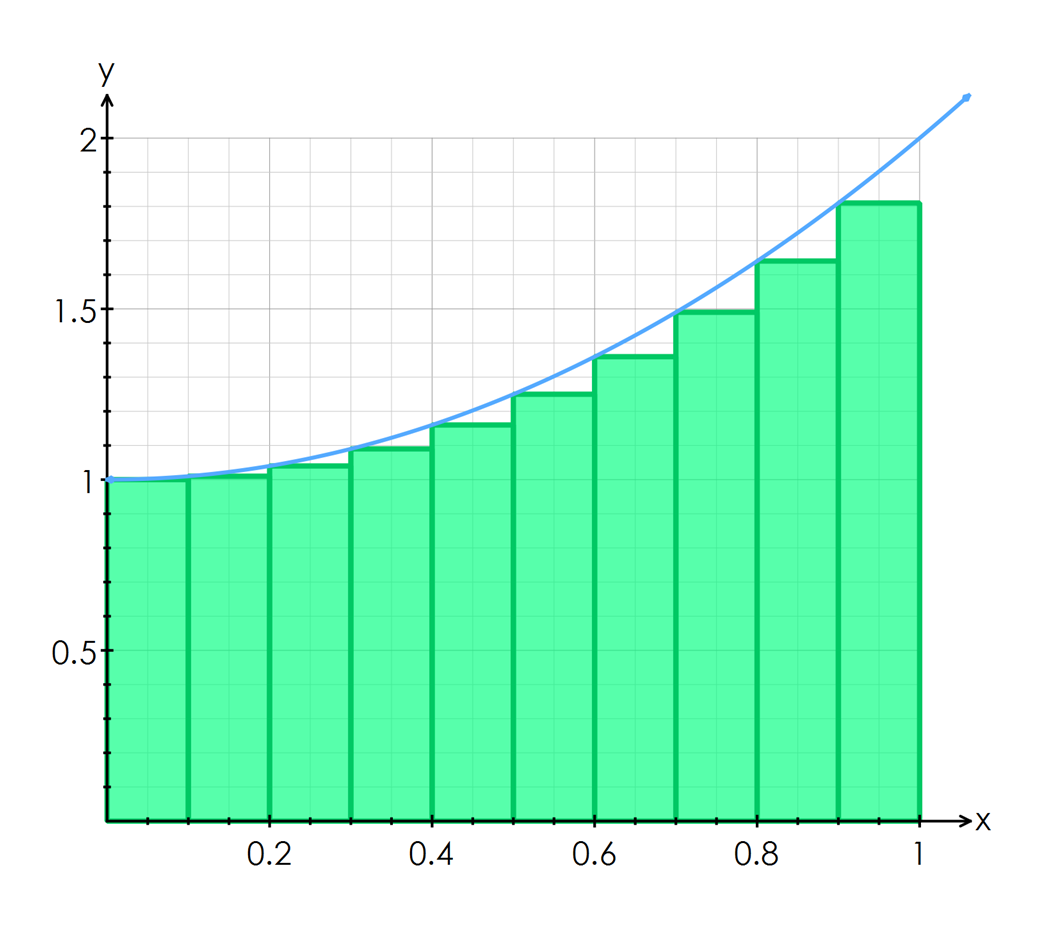
Have you ever wondered how to approximate the integral of a function using the trapezoid rule? It’s a simple yet powerful method that can give you a good estimate of the area under a curve.
By dividing the region into trapezoids and summing up their areas, you can get a close approximation of the integral. This method is especially useful when you don’t have a formula for the function you’re dealing with.
Approximate Integral Of X Trapezoid Rule Graph
Approximate Integral Of X Trapezoid Rule Graph
To use the trapezoid rule, start by dividing the interval of integration into equal segments. The more segments you use, the closer your approximation will be to the actual integral value.
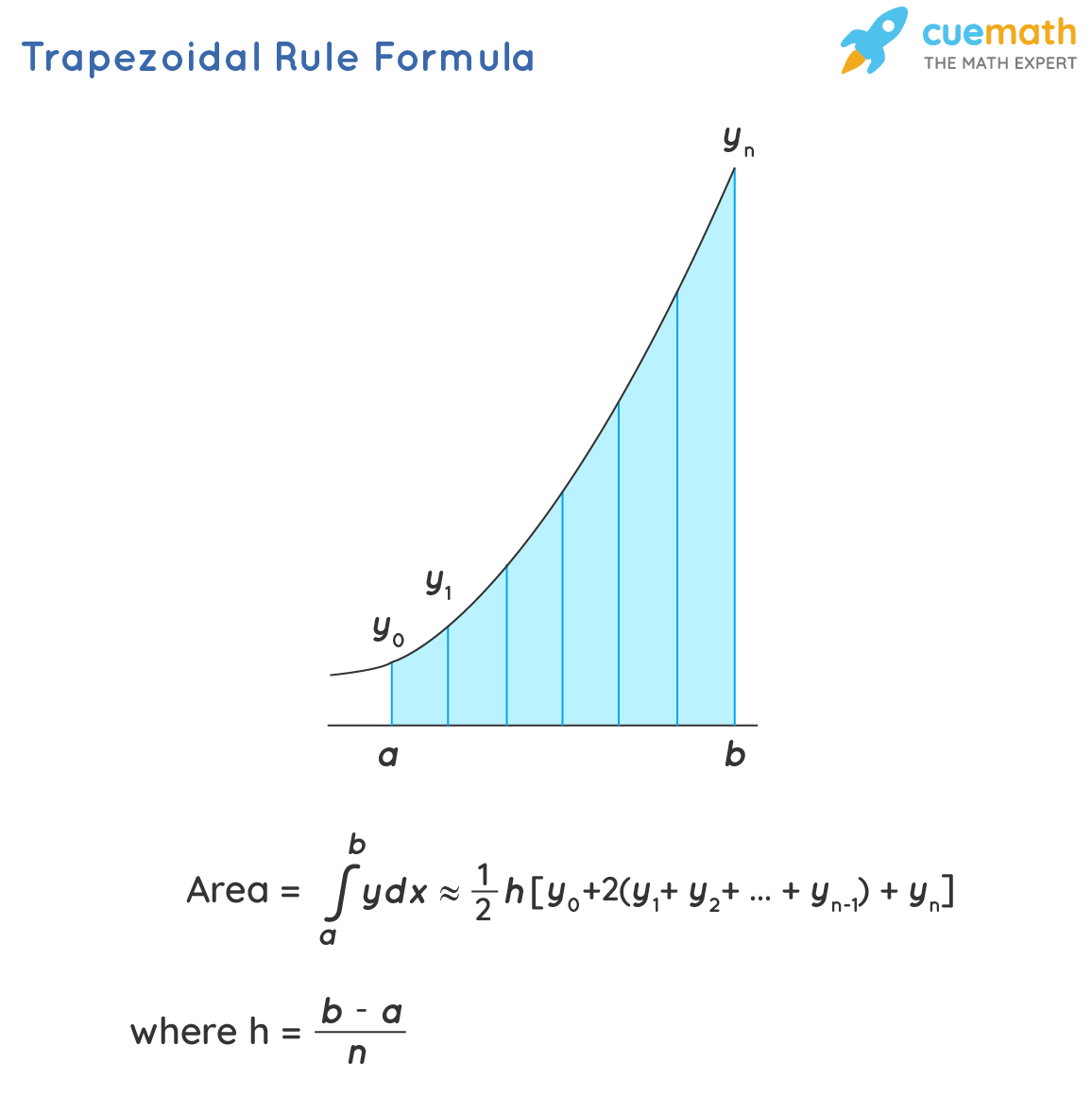
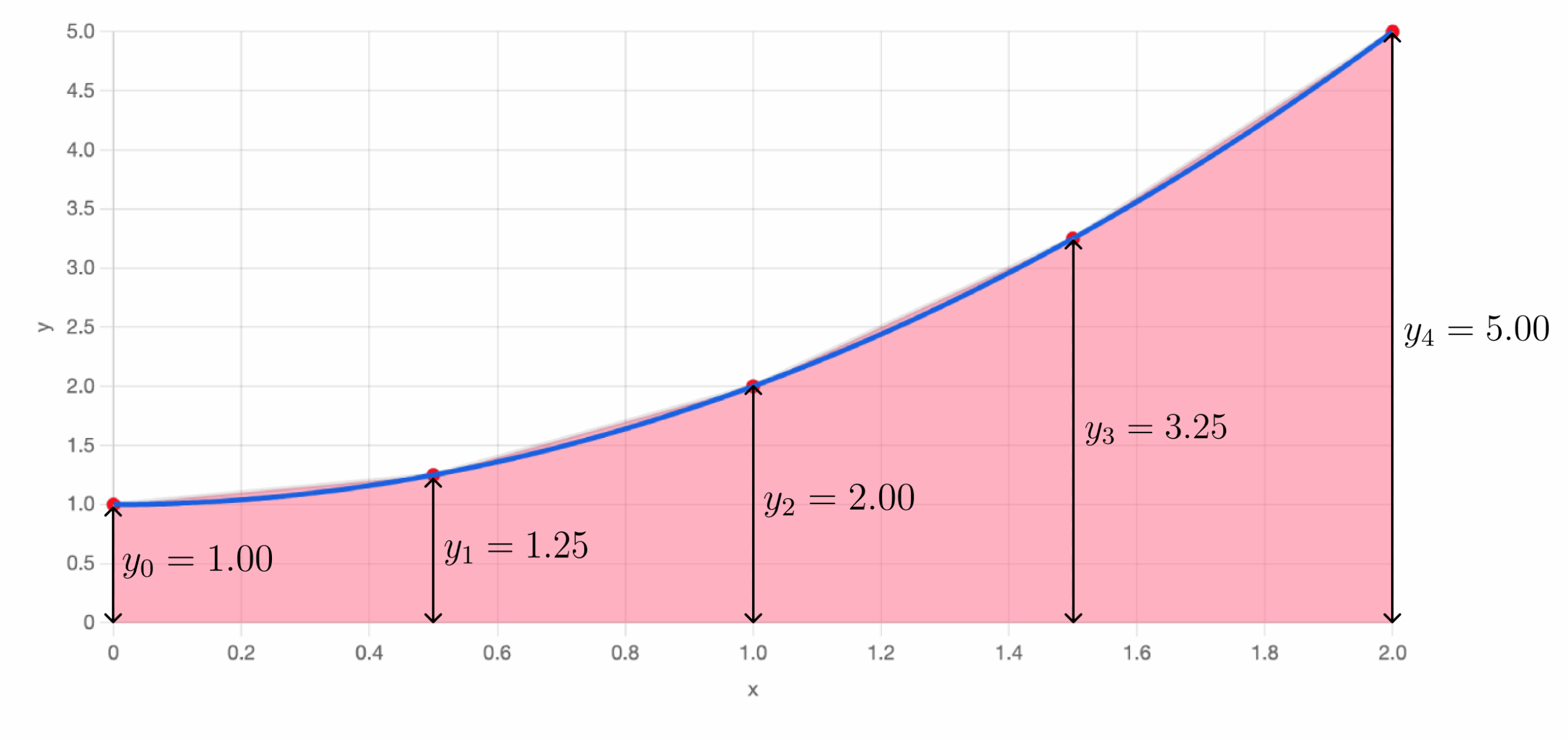
Next, find the height of each trapezoid by evaluating the function at the endpoints of each segment. Then, calculate the area of each trapezoid using the formula for the area of a trapezoid.
Finally, sum up the areas of all the trapezoids to get your approximation of the integral. This method is straightforward and easy to implement, making it a popular choice for numerical integration.
So, next time you need to find the integral of a function but don’t have a closed-form solution, give the trapezoid rule a try. It’s a handy tool to have in your mathematical toolbox and can help you solve a wide range of problems.
In conclusion, the trapezoid rule is a versatile technique for approximating integrals that doesn’t require advanced mathematical knowledge. By breaking down the region into trapezoids and summing their areas, you can quickly estimate the integral of a function. Give it a shot and see how useful it can be!
Trapezoidal Rule Formula Trapezoidal Formula
Trapezoidal Rule Calculator Academo Free Interactive Education