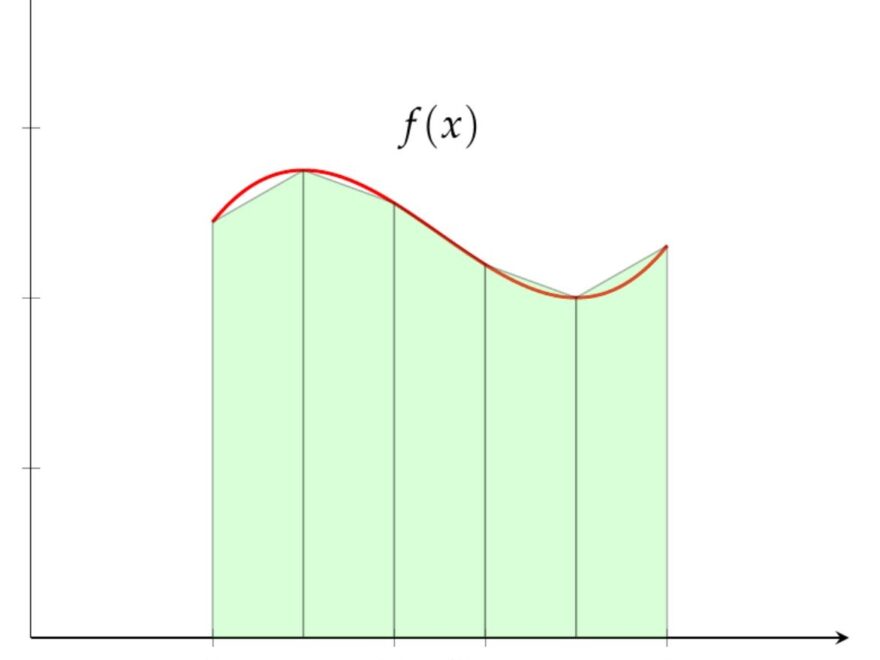
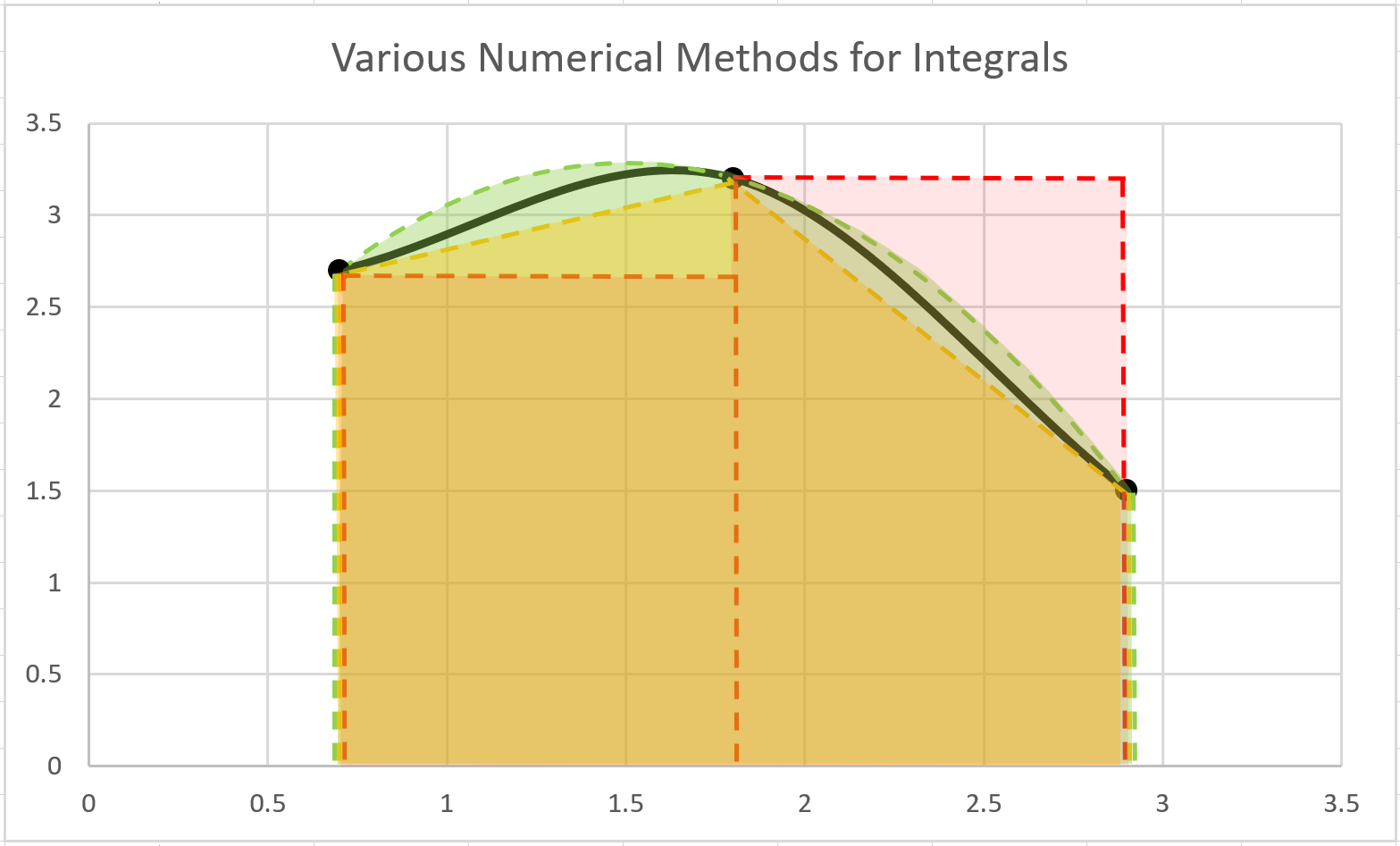
Numerical integration is a method used to approximate the definite integral of a function. One common technique is the Trapezoidal Method, which divides the area under a curve into trapezoids for estimation.
By using the Trapezoidal Method, we can calculate the area under a curve by approximating it with a series of trapezoids. This method is useful when we need to find the integral of a function for which we do not have a closed-form solution.
Numerical Integration Trapezoidal Method Graph
Numerical Integration Trapezoidal Method Graph
To apply the Trapezoidal Method, we divide the interval of integration into smaller subintervals and approximate the area under the curve using trapezoids. The more subintervals we use, the more accurate our approximation will be.
Once we have divided the interval into subintervals and approximated the area under the curve with trapezoids, we sum up the areas of all the trapezoids to get an estimate of the integral of the function over the given interval.
The Trapezoidal Method is a simple yet effective way to approximate integrals numerically. It is suitable for functions that are difficult to integrate analytically or when we need a quick estimation of the integral without going through complex calculations.
In conclusion, the Trapezoidal Method is a valuable tool in numerical integration, allowing us to approximate the area under a curve efficiently. By breaking down the interval into smaller segments and using trapezoids, we can obtain a close estimation of the integral of a function.
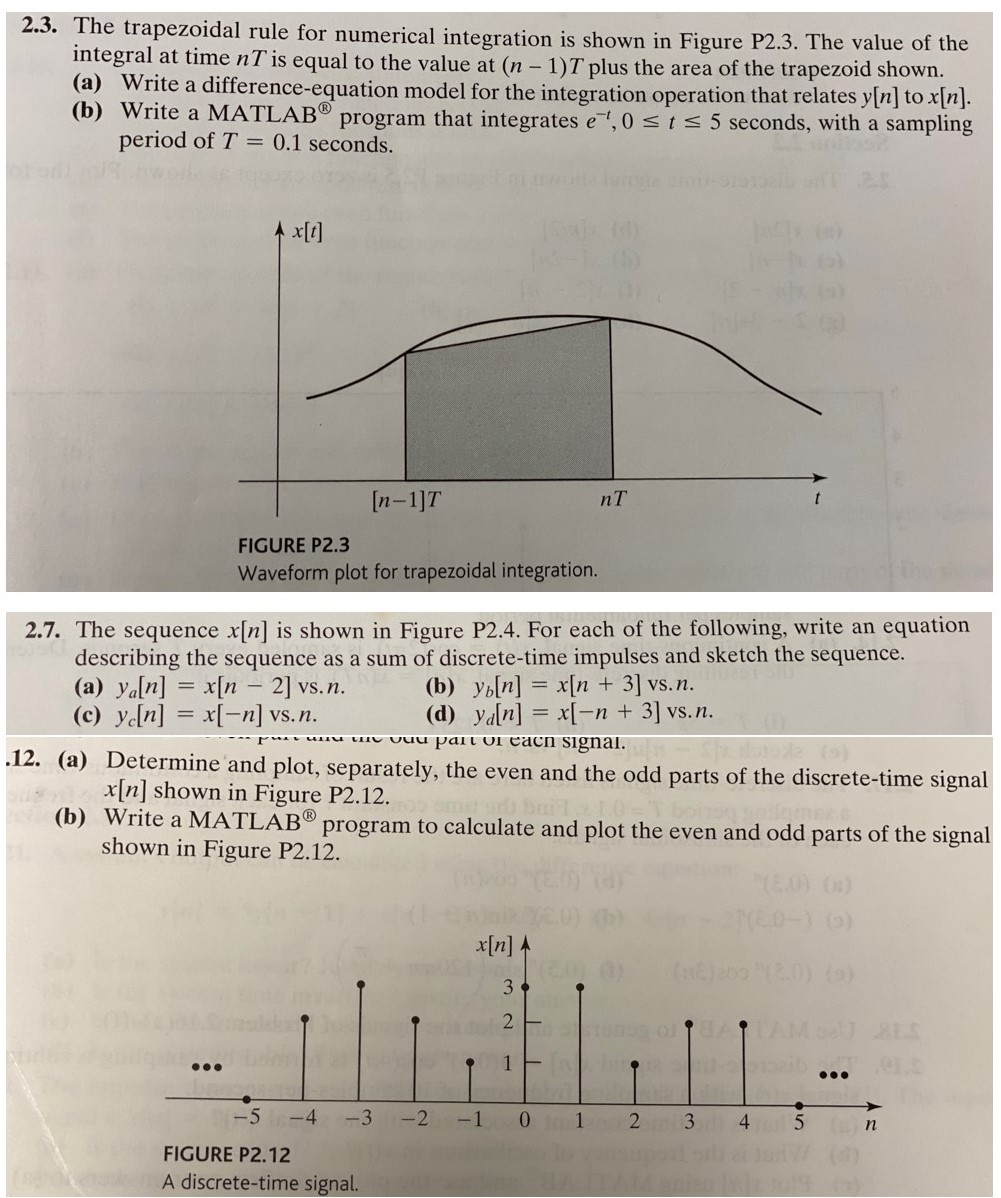
Solved 2 3 The Trapezoidal Rule For Numerical Integration Chegg