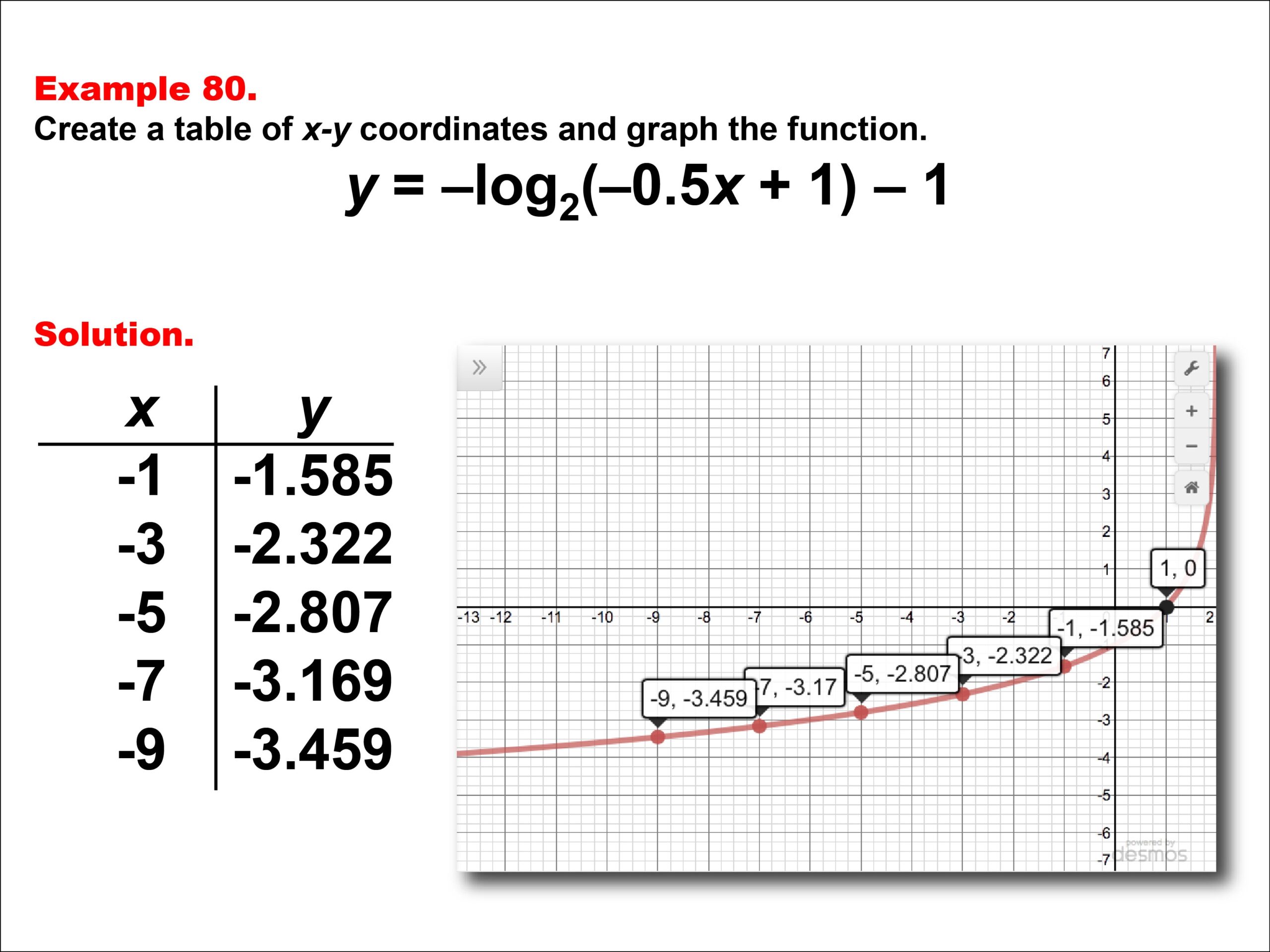
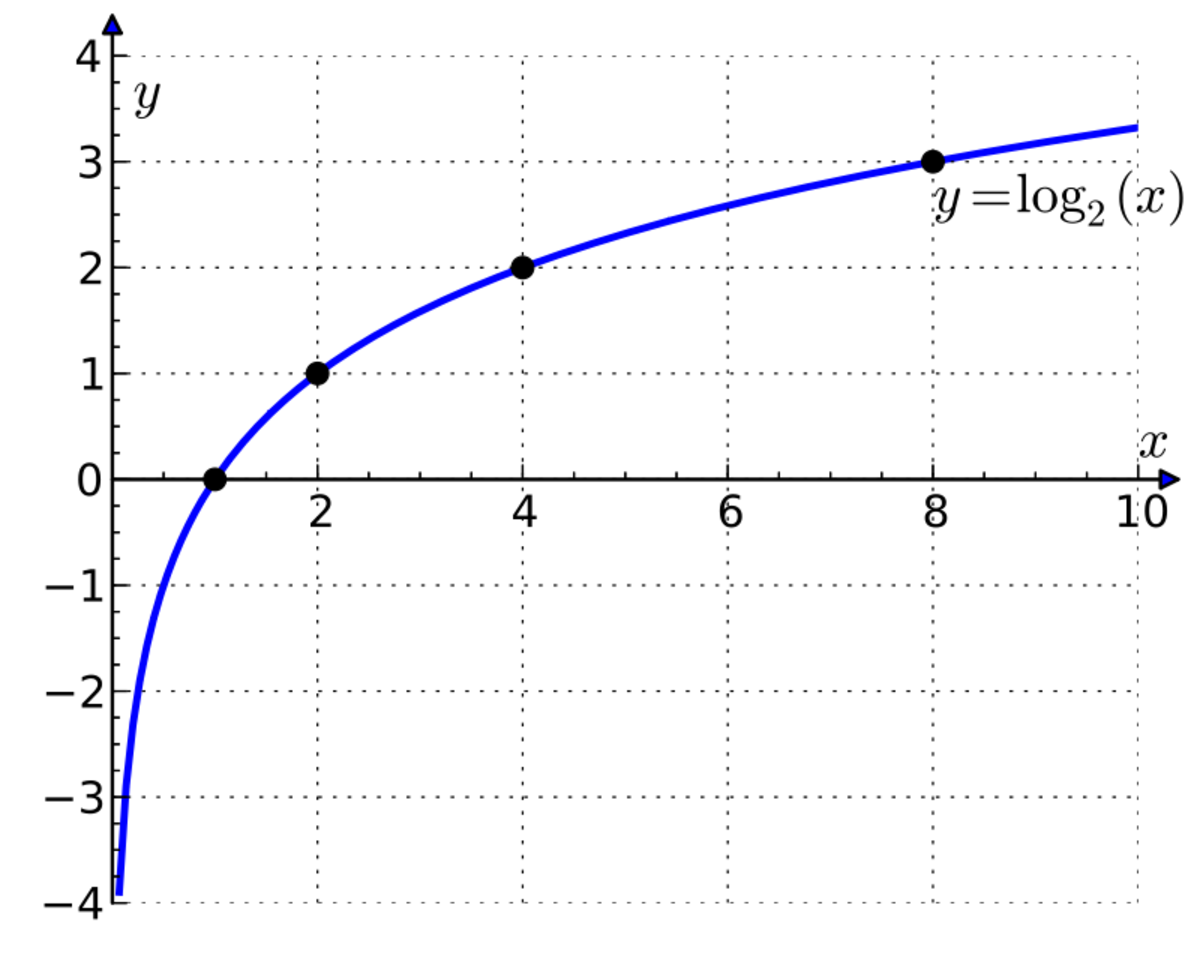
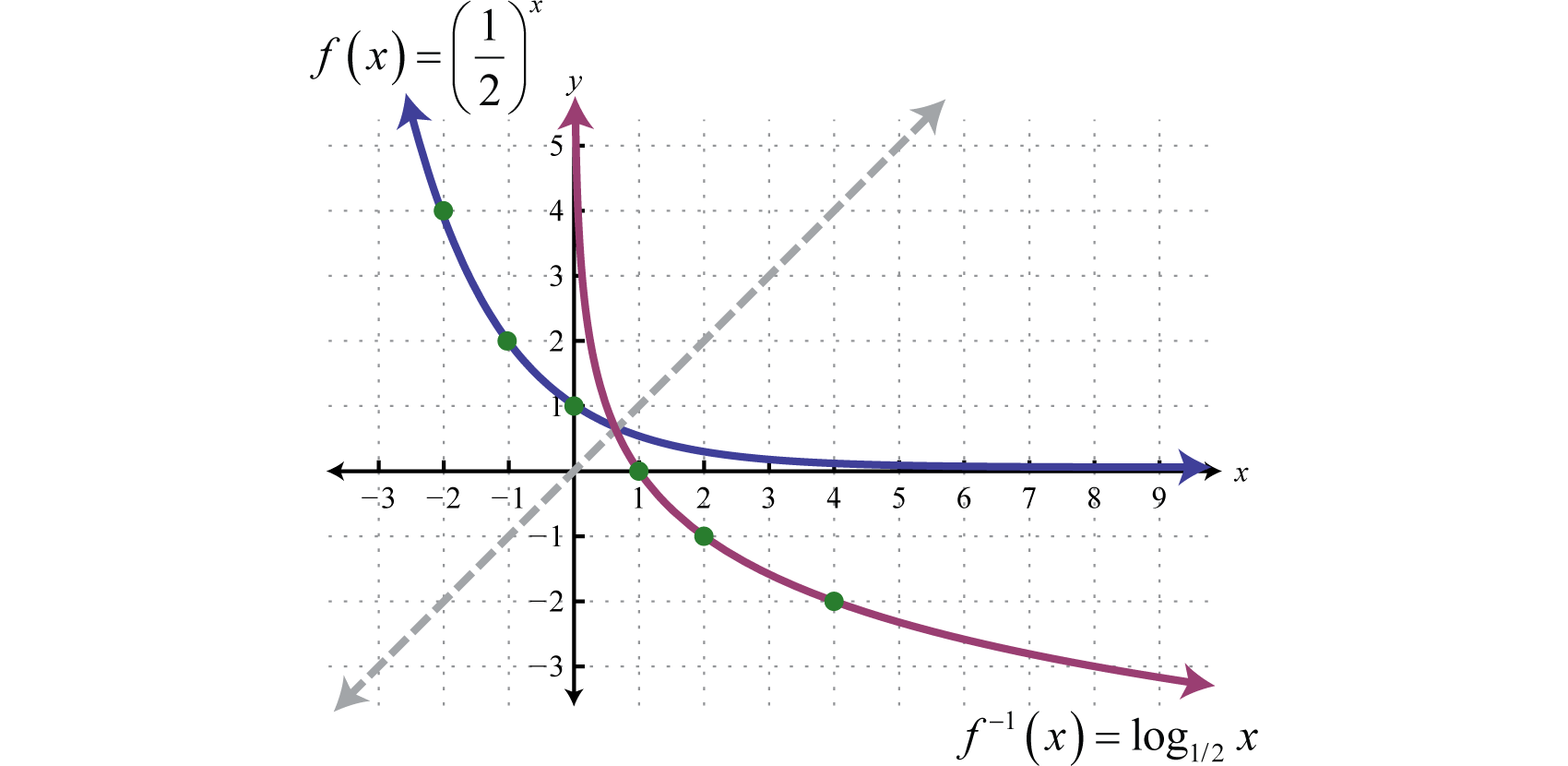
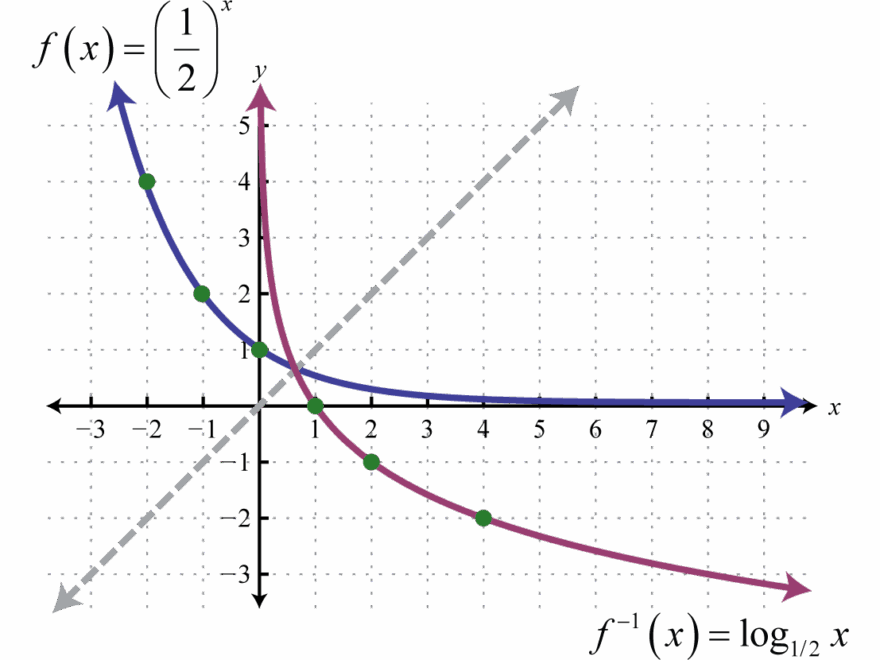Are you struggling to understand logarithmic functions and how to graph them? Don’t worry, we’ve got you covered! Logarithmic functions can be tricky to grasp at first, but with a little practice, you’ll be a pro in no time.
Whether you’re a student studying for a math exam or just someone curious about the world of logarithms, learning how to graph logarithmic functions can be a valuable skill to have. Let’s dive into some examples to help you better understand this mathematical concept.
Logarithmic Function Graph Examples
Logarithmic Function Graph Examples
Let’s start with a basic example of a logarithmic function: f(x) = log₂(x). In this function, the base is 2, which means that we are working with a logarithm base 2. When graphing this function, you’ll notice that it increases at a decreasing rate.
Now, let’s move on to a more advanced example: f(x) = log₄(x – 2). In this function, the base is 4, and there is a horizontal translation by 2 units to the right. The graph of this function will shift to the right by 2 units compared to the basic logarithmic function.
Another example to consider is the function f(x) = -log₃(x + 1). In this case, the negative sign in front of the logarithm indicates a reflection across the x-axis. The graph of this function will be a mirror image of the basic logarithmic function.
As you practice more examples and become familiar with the properties of logarithmic functions, graphing them will become second nature. Remember, practice makes perfect, so don’t be afraid to tackle more challenging examples to enhance your understanding of logarithmic functions.
Now that you’ve explored a few logarithmic function graph examples, you’re well on your way to mastering this mathematical concept. Keep practicing, stay curious, and don’t hesitate to seek help if you encounter any difficulties along the way. Happy graphing!
Rules Of Logarithms And Exponents With Worked Examples And Problems HubPages
Logarithmic Functions And Their Graphs