Are you struggling with understanding the Trapezoid Rule in calculus? Don’t worry, you’re not alone! Many students find this concept challenging at first, but with a little practice and guidance, you’ll be a pro in no time.
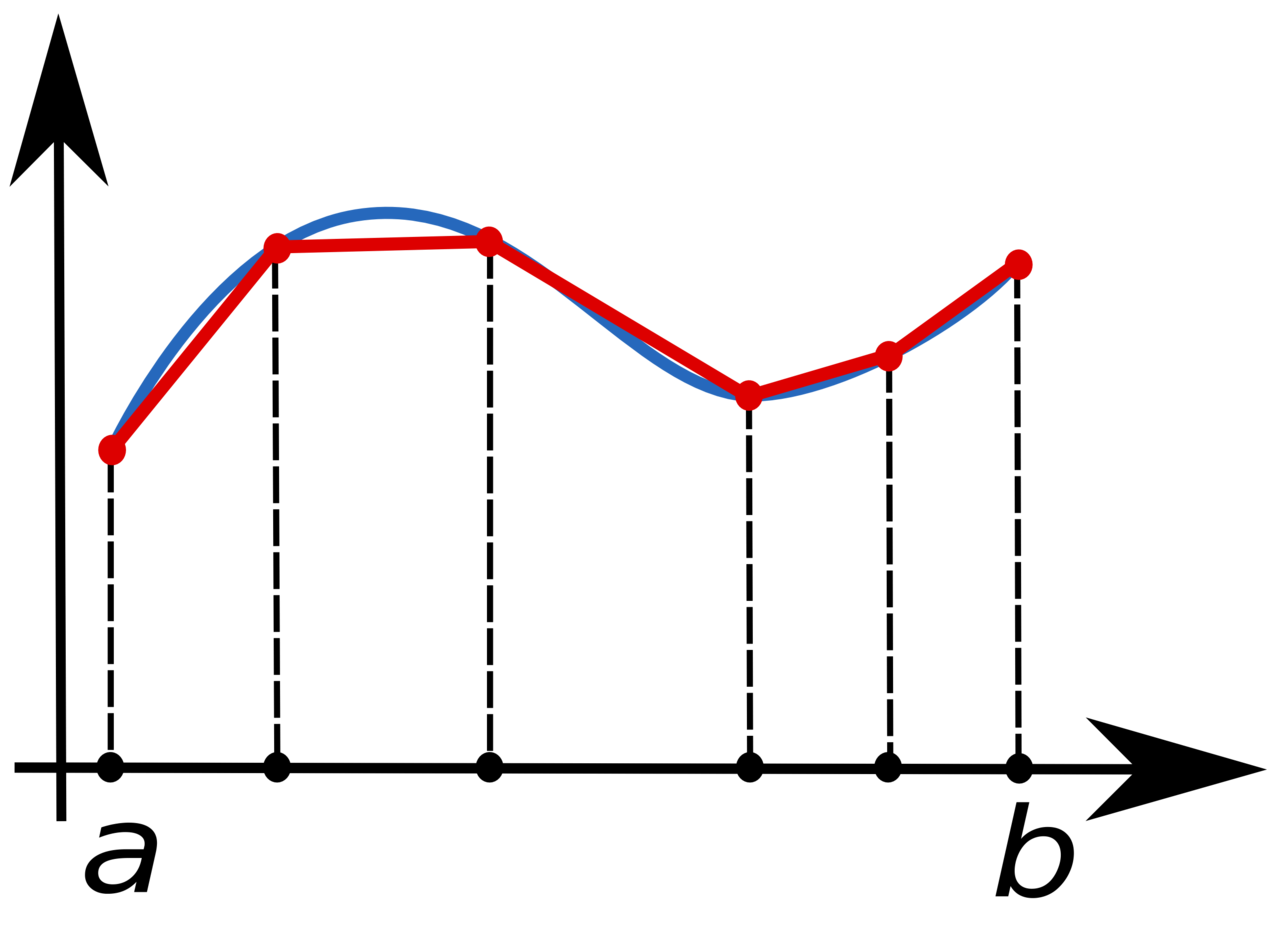
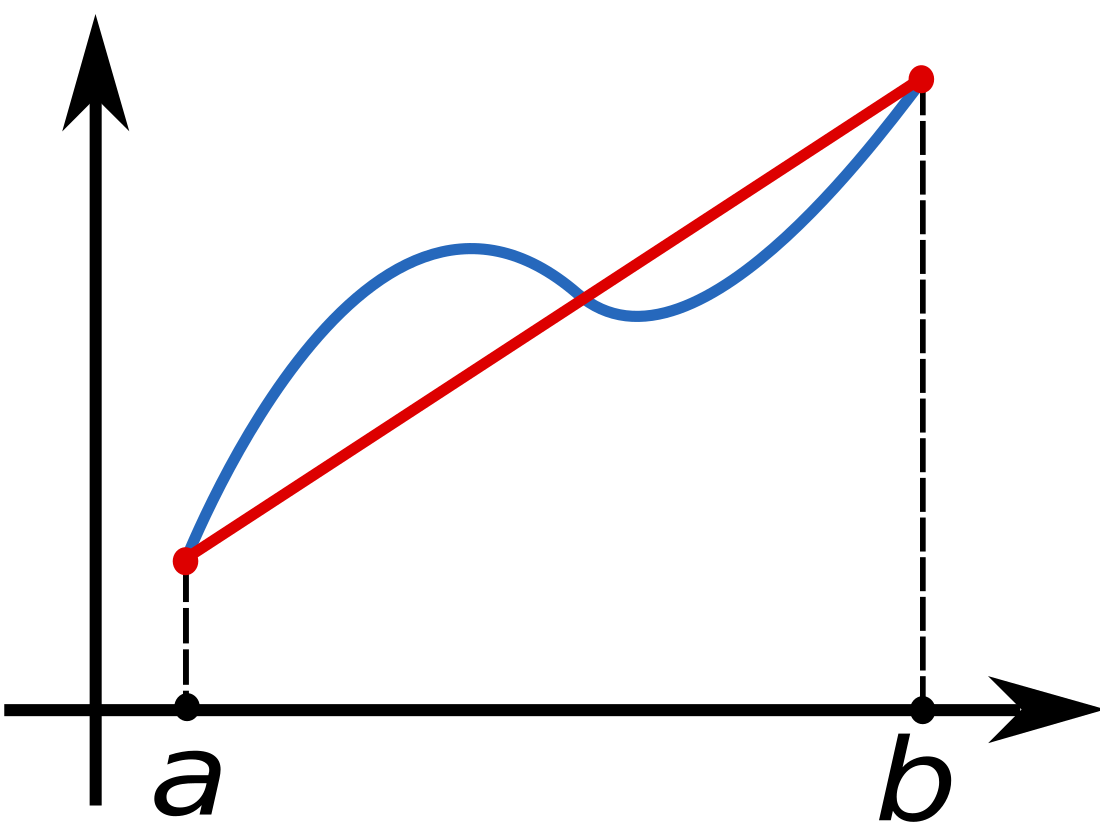
In simple terms, the Trapezoid Rule is a method used to approximate the area under a curve by dividing it into trapezoids. By summing up the areas of these trapezoids, you can get a good estimate of the total area under the curve.
Trapezoid Rule Using A Graph
Trapezoid Rule Using A Graph
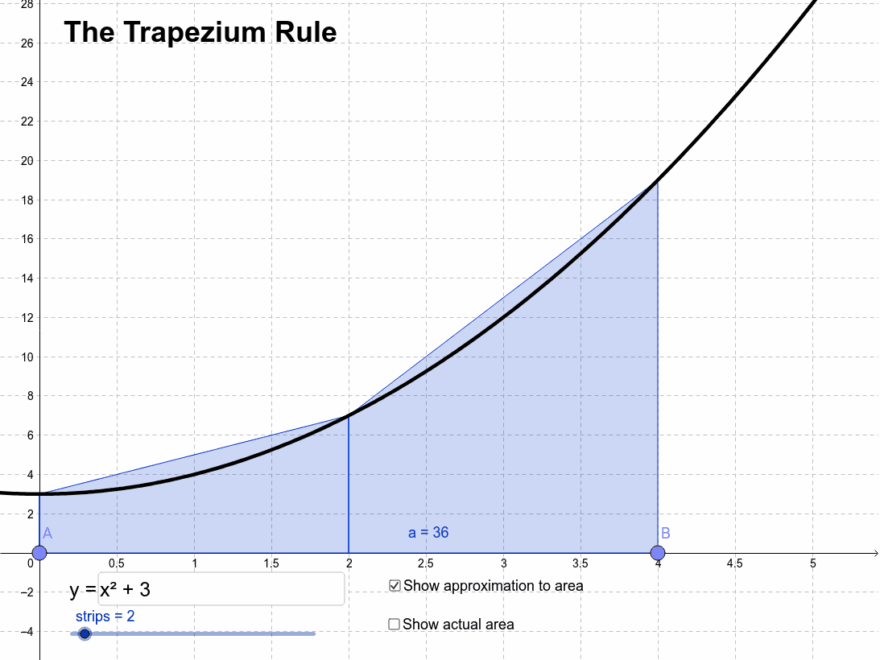
To use the Trapezoid Rule with a graph, you first need to plot the function you’re working with on a graph. Then, you divide the area under the curve into smaller trapezoids by drawing vertical lines from the curve to the x-axis.
Next, calculate the width of each trapezoid by finding the difference between the x-values of the two points where the vertical lines intersect the curve. Then, find the height of each trapezoid by taking the average of the y-values at those two points.
Once you have the width and height of each trapezoid, you can calculate the area of each trapezoid using the formula for the area of a trapezoid: 0.5 * (base1 + base2) * height. Finally, sum up the areas of all the trapezoids to get an approximation of the total area under the curve.
Practice makes perfect when it comes to mastering the Trapezoid Rule. The more you work with it and understand its principles, the easier it will become. So, don’t get discouraged if you don’t grasp it right away – keep practicing and seeking help when needed. You’ll get there!
Trapezoidal Rule Wikiwand
Approximating Area The Trapezium Rule GeoGebra